1. はじめに
このセクションは規定仕様ではありません。
CSSの視覚的フォーマットモデルは、各要素が配置される座標系について説明しています。この座標空間内の位置やサイズは、ピクセルで表現されると考えることができ、原点から右方向および下方向に正の値が進みます。
この座標空間は、transformプロパティによって変更できます。transformを使うことで、要素を移動(translate)、回転(rotate)、拡大縮小(scale)することができます。
1.1. モジュール間の相互作用
このモジュールは、これらのプロパティが適用された要素の視覚的レンダリングに影響するCSSプロパティ群を定義します。これらの効果は、要素が視覚的フォーマットモデル([CSS2])によってサイズ・位置が決定された後に適用されます。これらのプロパティの一部の値は、包含ブロックや積み重ねコンテキストの生成を引き起こします。
transformは、fixed値が指定されたbackground-attachmentプロパティを持つ要素の背景描画に影響します([CSS3BG]参照)。
transformは、Element Interface Extensionsで返されるclient rectangle(getClientRects()およびgetBoundingClientRect())にも影響します([CSSOM-VIEW]参照)。
transformは、スクロール可能なオーバーフロー領域の計算にも影響します([CSS-OVERFLOW-3]参照)。
1.2. CSS値
本仕様はCSSプロパティ定義規約([CSS2])に従います。 本仕様で定義されていない値型はCSS Values & Units [CSS-VALUES-3]で定義されています。 他のCSSモジュールによってこれらの値型の定義が拡張される場合もあります。
各プロパティ定義に記載されたプロパティ固有の値に加え、 本仕様で定義されるすべてのプロパティはCSS全体キーワードも値として受け付けます。 可読性のため、明示的な記載は省略しています。
2. 用語
本仕様で使用される用語は、このセクションで定義された意味を持ちます。
- 変形可能要素
-
変形可能要素は以下のカテゴリのいずれかに属する要素です:
-
CSSボックスモデルでレイアウトが制御されるすべての要素(ただし、非置換インラインボックス、table-columnボックス、table-column-groupボックスは除く)[CSS2]、
-
すべてのSVGペイントサーバー要素、clipPath要素、およびSVGレンダリング可能要素(ただし、テキストコンテンツ要素の子孫要素は除く)[SVG2]。
-
- 変形要素
-
transformプロパティの算出値がnone以外の要素。
- ユーザー座標系
- ローカル座標系
-
一般的に、座標系は現在のキャンバス上の位置と距離を定義します。現在のローカル座標系(ユーザー座標系)は、現在有効で、座標や長さがどのように配置・計算されるかを定義する座標系です。 現在のユーザー座標系の原点は、reference box(transform-boxプロパティで指定))の左上にあります。パーセンテージ値はこのreference boxの寸法に対する相対値です。1単位は1CSSピクセルです。
- 変形行列
-
ある座標系から別の座標系への数学的なマッピングを定義する行列。これはtransformプロパティとtransform-originプロパティの値から、以下のように算出されます。
- 現在の変形行列 (CTM)
- 2D行列
-
3x2変形行列、または m31, m32, m13, m23, m43, m14, m24, m34 が0で、m33, m44が1である4x4行列。
- 単位変形関数
-
4x4の単位行列と等価な変形関数(変形関数の数学的記述参照)。単位変形関数の例:translate(0)、translateX(0)、translateY(0)、scale(1)、scaleX(1)、scaleY(1)、rotate(0)、skew(0, 0)、skewX(0)、 skewY(0)、matrix(1, 0, 0, 1, 0, 0)など。
- ポストマルチプライ
- ポストマルチプライされた
-
項Aを項Bでポストマルチプライした場合は A · B となります。
- プリマルチプライ
- プリマルチプライされた
-
項Aを項Bでプリマルチプライした場合は B · A となります。
- 乗算
-
項Aに項Bを乗算する場合は A · B となります。
3. 変形レンダリングモデル
このセクションは規定仕様です。
transformプロパティにnone以外の値を指定すると、その要素に新しいローカル座標系が確立されます。要素が本来レンダリングされる位置からそのローカル座標系へのマッピングは、要素の変形行列によって表されます。
変形行列は、transformプロパティとtransform-originプロパティから次のように算出されます:
-
単位行列から開始します。
-
transform-originの算出X・Y値で移動します。
-
transformプロパティの各変形関数で左から右に順番に乗算します。
-
transform-originの算出X・Y値の符号を反転して移動します。
ある要素にtransformプロパティ(none以外)が設定されています。
div {
transform-origin : 0 0 ;
transform : translate ( -10 px , -20 px ) scale ( 2 ) rotate ( 45 deg );
}
transform-originプロパティは0 0に設定されており、省略可能です。変形行列 TMは、<translate()>、<scale()>、<rotate()> <transform-function>をポストマルチプライして算出されます。

transformは変形可能要素に適用されます。
座標空間は2軸からなる座標系であり、X軸は水平方向右側に増加し、Y軸は垂直方向下側に増加します。
変形は累積的です。すなわち、要素は親の座標系内に自分のローカル座標系を確立します。
要素のローカル座標系の座標ペアxlocal、ylocalを持つ点plocalを親の座標系にマッピングするには、要素の変形行列 TMにplocalをポストマルチプライします。結果は、親のローカル座標系での座標ペアxparent、yparentを持つ点pparentです。
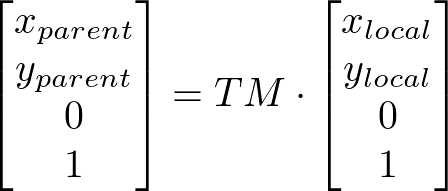
利用者の視点からは、要素は祖先のtransformプロパティをすべて累積し、さらに自身のローカルtransformも適用します。これらのtransformの累積によって、要素の現在の変形行列(CTM)が定義されます。
現在の変形行列は、ビューポート座標系から始まり、要素の変形行列まで、すべての変形行列をポストマルチプライして算出されます。
< svg xmlns = "http://www.w3.org/2000/svg" >
< g transform = "translate(-10, 20)" >
< g transform = "scale(2)" >
< rect width = "200" height = "200" transform = "rotate(45)" />
</ g >
</ g >
</ svg >
-
translate(-10, 20)は変形行列T1として算出されます。
-
scale(2)は変形行列T2として算出されます。
-
rotate(45)は変形行列T3として算出されます。
SVGrect要素のCTMは、T1、T2、T3を順に乗算した結果です。
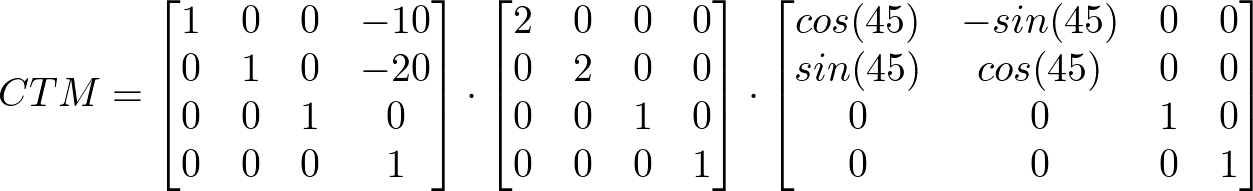
SVGrect要素のローカル座標系の座標ペアxlocal、ylocalを持つ点plocalをビューポート座標系にマッピングするには、要素の現在の変形行列 CTMにplocalをポストマルチプライします。結果は、ビューポート座標系の座標ペアxviewport、yviewportを持つ点pviewportとなります。
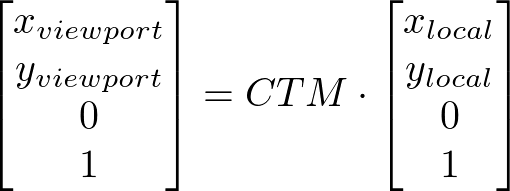
注意: 変形は視覚的レンダリングには影響しますが、CSSレイアウトにはオーバーフロー以外の影響はありません。transformは、Element Interface Extensions(getClientRects()やgetBoundingClientRect())でも考慮されます([CSSOM-VIEW]参照)。
div {
height : 100 px ; width : 100 px ;
transform-origin : 50 px 50 px ;
transform : rotate ( 45 deg );
}
transform-originプロパティはX・Y方向にそれぞれ50ピクセル原点を移動させます。transformは、原点を中心に要素を時計回りに45°回転させます。すべての変形関数適用後、原点の移動はX・Y方向とも-50ピクセルだけ戻されます。
div {
height : 100 px ; width : 100 px ;
transform : translate ( 80 px , 80 px ) scale ( 1.5 , 1.5 ) rotate ( 45 deg );
}
見かけ上、div要素は左下方向に80px移動し、150%拡大され、最後に45°回転します。
各<transform-function>は、対応する4x4行列で表現できます。divボックスの座標空間から親要素の座標空間へ点をマッピングするには、これらの変形を逆順で乗算します:
詳細は変形関数リストを参照してください。
注意: 上記と同じレンダリングは、等価なtransformを入れ子要素で記述しても得られます:
< div style = "transform: translate(80px, 80px)" >
< div style = "transform: scale(1.5, 1.5)" >
< div style = "transform: rotate(45deg)" ></ div >
</ div >
</ div >
CSSボックスモデルでレイアウトされる要素の場合、transformプロパティは周囲のコンテンツのフローには影響しませんが、オーバーフロー領域の範囲には影響します。この挙動は、相対位置によって要素がオフセットされる場合と似ています。したがって、overflow プロパティの値がscrollやautoの場合、変形によって可視領域外に出たコンテンツを表示するためにスクロールバーが表示されます。特に、transformはオーバーフロー領域のサイズを拡張することがあります(縮小はしません)。このサイズは、変形前後の要素の境界の合計として計算されます。
CSSボックスモデルでレイアウトされる要素の場合、transformプロパティがnone以外の値になると積み重ねコンテキストが作成されます。実装では、このレイヤーを親の積み重ねコンテキスト内で、z-index: 0のpositioned要素と同じ積み重ね順で描画しなければなりません。transform付き要素がpositionedの場合は、z-indexプロパティが[CSS2]の記述通り適用されますが、autoは常に0とみなされます(新しい積み重ねコンテキストが必ず作成されるため)。
CSSボックスモデルでレイアウトされる要素の場合、transformプロパティがnone以外の値になると、その要素はすべての子孫のための包含ブロックも確立します。paddingボックスが、絶対位置指定子・固定位置指定子・固定背景添付の子孫のレイアウトに使われます。
< style >
# container {
width : 300 px ;
height : 200 px ;
border : 5 px dashed black ;
padding : 5 px ;
overflow : scroll ;
}
# bloat {
height : 1000 px ;
}
# child {
right : 0 ;
bottom : 0 ;
width : 10 % ;
height : 10 % ;
background : green ;
}
</ style >
< div id = "container" style = "transform:translateX(5px);" >
< div id = "bloat" ></ div >
< div id = "child" style = "position:fixed;" ></ div >
</ div >
対して
< div id = "container" style = "position:relative; z-index:0; left:5px;" >
< div id = "bloat" ></ div >
< div id = "child" style = "position:absolute;" ></ div >
</ div >
固定背景は、ルート要素に指定されたtransformの影響を受けます。それ以外のtransformが適用された要素(自身または祖先要素にtransformが適用された要素)では、fixed値のbackground-attachmentプロパティは、scroll値として扱われます。background-attachmentの算出値自体は変化しません。
注意: ルート要素が変形される場合、その変形はキャンバス全体(ルート要素に指定された背景も含む)に適用されます。ルート要素の背景描画領域はキャンバス全体(無限)なので、変形によって元々画面外だった背景部分が表示されることがあります。例えば、ルート要素の背景が繰り返しドットだった場合、scale(0.5)を指定すると、ドットは半分の大きさになりますが、数は2倍になるため、ビュー ポート全体をカバーし続けます。
4. transformプロパティ
変形は、transformプロパティを通じて、要素が描画される座標系に適用されます。 このプロパティは変形関数のリストを含みます。座標系の最終的な変形値は、リスト内の各関数を変形関数の数学的記述で定義されているように対応する行列に変換し、それらの行列を乗算することで得られます。
| 名前: | transform |
|---|---|
| 値: | none | <transform-list> |
| 初期値: | none |
| 適用対象: | 変形可能要素 |
| 継承: | no |
| パーセンテージ: | reference boxのサイズに依存 |
| 算出値: | 指定通り。ただし長さは絶対値化される |
| 正規順序: | 文法に準拠 |
| アニメーション型: | transformリスト。補間規則参照 |
transformの算出値がnone以外の場合は、§3 変形レンダリングモデルで説明されているように、包含ブロックや積み重ねコンテキストに影響します。
<transform-list> = <transform-function>+
4.1. <transform-function>のシリアライズ
<transform-function>のシリアライズは、それぞれの個々の文法に従い、文法で記述された順序で行い、可能な限り<calc()>式や<calc()>変形を避け、意味が変わらない範囲で構成要素を省略し、スペース区切りトークンは1つのスペースで結合し、シリアライズしたカンマの後には必ず1つのスペースを入れること。
4.2. <transform-list>の算出値のシリアライズ
算出値としての<transform-list>は、次のアルゴリズムにより1つの<matrix()>関数としてシリアライズされます:
-
transformを単位行列で初期化した4x4行列とする。transformの要素m11、m22、m33、m44は1に、他の要素は0に設定する。
-
<transform-function>すべてを<transform-list>でtransformにポストマルチプライする。
-
transformを<matrix()>関数としてシリアライズする。
5. transform-originプロパティ
| 名前: | transform-origin |
|---|---|
| 値: | [ left | center | right | top | bottom | <length-percentage> ] | [ left | center | right | <length-percentage> ] [ top | center | bottom | <length-percentage> ] <length>? | [[ center | left | right ] && [ center | top | bottom ]] <length>? |
| 初期値: | 50% 50% |
| 適用対象: | 変形可能要素 |
| 継承: | no |
| パーセンテージ: | reference boxのサイズに依存 |
| 算出値: | background-position参照 |
| 正規順序: | 文法に準拠 |
| アニメーション型: | 算出値による |
transformプロパティとtransform-originプロパティの値は、上記のように変形行列の計算に使われます。
値が1つだけ指定された場合は、2つ目の値はcenterとみなします。値が1つまたは2つ指定された場合、3つ目の値は0pxとみなします。
2つ以上の値が定義され、かつキーワード値が使われていない、または唯一使われているキーワードがcenterの場合、1つ目の値は水平方向の位置(またはオフセット)、2つ目は垂直方向の位置(またはオフセット)を表します。3つ目の値は常にZ方向の位置(またはオフセット)を表し、型は<length>でなければなりません。
- <length-percentage>
-
水平方向のオフセットのパーセンテージはreference boxの幅に対する相対値です。垂直方向のオフセットのパーセンテージはreference boxの高さに対する相対値です。水平方向・垂直方向オフセットの値は、reference boxの左上隅からのオフセットを表します。
- <length>
-
長さ値は固定長のオフセットを与えます。水平方向・垂直方向オフセットの値は、reference boxの左上隅からのオフセットを表します。
- top
-
垂直方向の位置が0%に算出されます。
- right
-
水平方向の位置が100%に算出されます。
- bottom
-
垂直方向の位置が100%に算出されます。
- left
-
水平方向の位置が0%に算出されます。
- center
-
水平方向の位置がそれ以外に指定されていなければ50%(left 50%)、垂直方向の位置が指定されていれば50%(top 50%)に算出されます。
CSSレイアウトボックスを持たないSVG要素の場合、初期のused valueは0 0となります。これは、UAスタイルシートに以下が含まれているかのように扱われます:
*:not(svg), *:not(foreignObject) > svg {
transform-origin : 0 0 ;
}
transform-originプロパティは、resolved value special case property(heightと同様)です。[CSSOM]
6. 変形基準ボックス:transform-boxプロパティ
| 名前: | transform-box |
|---|---|
| 値: | content-box | border-box | fill-box | stroke-box | view-box |
| 初期値: | view-box |
| 適用対象: | 変形可能要素 |
| 継承: | no |
| パーセンテージ: | N/A |
| 算出値: | 指定キーワード |
| 正規順序: | 文法に準拠 |
| アニメーション型: | 離散 |
transformプロパティおよびtransform-originプロパティで定義されたすべての変形は、要素の位置と寸法に対して基準ボックスを基準にして行われます。基準ボックスは以下のいずれかで指定されます:
- content-box
-
コンテンツボックスを基準ボックスとして使用します。テーブルの基準ボックスは、そのテーブルラッパーボックスのボーダーボックスであり、テーブルボックス自体ではありません。
- border-box
-
ボーダーボックスを基準ボックスとして使用します。テーブルの基準ボックスは、そのテーブルラッパーボックスのボーダーボックスであり、テーブルボックス自体ではありません。
- fill-box
-
オブジェクトバウンディングボックスを基準ボックスとして使用します。
- stroke-box
-
ストロークバウンディングボックスを基準ボックスとして使用します。
- view-box
-
最も近いSVGビューポートを基準ボックスとして使用します。
SVG
pattern
要素の場合、基準ボックスは
patternUnits
属性によって定義されます [SVG2]。
SVG linearGradientおよびradialGradient要素の場合、基準ボックスは
gradientUnits
属性によって定義されます [SVG2]。
SVG clipPath要素の場合、基準ボックスは
clipPathUnits
属性によって定義されます [CSS-MASKING]。
基準ボックスは、transform-originプロパティで指定された原点に追加のオフセットを加えます。
CSSレイアウトボックスを持たないSVG要素の場合、used valueがcontent-boxの場合はfill-boxとなり、border-boxの場合はstroke-boxとなります。
CSSレイアウトボックスを持つ要素の場合、used valueがfill-boxの場合はcontent-boxとなり、 stroke-boxやview-boxの場合はborder-boxとなります。
7. SVG transform属性
7.1. SVG表示属性
transform-originCSSプロパティも表示属性であり、既存の表示属性リストを拡張します [SVG2]。
SVG 2はtransform、
patternTransform、
gradientTransform
属性を表示属性として定義し、CSSのtransformプロパティで表現されます [SVG2]。
CSSカスケードへの参加は、SVG仕様で定義された表示属性の詳細度(specificity)によって決まります。SVGによれば、ユーザーエージェントは概念的に表示属性用の新しい著者用スタイルシートを挿入し、それが著者用スタイルシート集合の最初になります [SVG2]。
<svg xmlns= "http://www.w3.org/2000/svg" >
<style>
.container {
transform: translate(100px, 100px);
}
</style>
<g class= "container" transform= "translate(200 200)" >
<rect width= "100" height= "100" fill= "blue" />
</g>
</svg>
CSSカスケードへの参加により、transformスタイルプロパティがtransform属性を上書きします。そのため、containerは水平方向・垂直方向とも100pxだけ移動し、200pxにはなりません。
7.2. SVG transform属性の構文
後方互換性の理由から、transform、
patternTransform、
gradientTransform
属性の構文は、CSSのtransformプロパティの構文とは異なります。属性では、CSSのtransformプロパティのために定義された追加の<transform-function>はサポートされていません。具体的には、<translateX()>、<translateY()>、<scaleX()>、<scaleY()>、<skew()>は、transform、
patternTransform、
gradientTransform
属性ではサポートされません。
以下のリストは、transform、patternTransform、gradientTransform属性の値を、Backus-Naur Form (BNF)で定義したもので、説明的なレールロード図も続きます。以下の記法が使われます:
-
*: 0回以上
-
+: 1回以上
-
?: 0回または1回
-
(): グループ化
-
|: 選択肢の区切り
-
ダブルクォートはリテラルを囲みます。リテラルは英字、左括弧、右括弧からなります [CSS-SYNTAX-3]。
-
<number-token>はCSS Syntaxモジュールで定義されています [CSS-SYNTAX-3]。
注意: この構文はユーザーエージェントの実装動作を反映しており、SVG 1.1で定義された構文とは異なります。
- left parenthesis (
- U+0028 左括弧
- right parenthesis )
- U+0029 右括弧
- comma
- U+002C カンマ
- wsp
- U+000A ラインフィード、U+000D キャリッジリターン、U+0009 タブ、またはU+0020 スペースのいずれか
- comma-wsp
-
(wsp+ comma? wsp*) | (comma wsp*)
- translate
-
"translate" wsp* "(" wsp* number ( comma-wsp? number )? wsp* ")" - scale
-
"scale" wsp* "(" wsp* number ( comma-wsp? number )? wsp* ")" - rotate
-
"rotate" wsp* "(" wsp* number ( comma-wsp? number comma-wsp? number )? wsp* ")" - skewX
-
"skewY" wsp* "(" wsp* number wsp* ")" - skewY
-
"skewY" wsp* "(" wsp* number wsp* ")" - matrix
-
"matrix" wsp* "(" wsp* number comma-wsp? number comma-wsp? number comma-wsp? number comma-wsp? number comma-wsp? number wsp* ")" - transform
-
matrix | translate | scale | rotate | skewX | skewY
- transforms
-
transform | transform comma-wsp transforms
- transform-list
-
wsp* transforms? wsp*
7.3. SVG変形関数
上記の構文で定義されるtransform、
patternTransform、
gradientTransform
属性のSVG変形関数は、以下のようにCSS <transform-function>にマッピングされます:
| SVG変形関数 | CSS <transform-function> | 補足 |
|---|---|---|
| translate | <translate()> | 数値はCSSの<length> 型としてpx単位で解釈されます。 |
| scale | <scale()> | |
| rotate | <rotate()> | 単一値のみ。数値はCSSの<angle>型としてdeg単位で解釈されます。 |
| skewX | <skewX()> | 数値はCSSの<angle>型としてdeg単位で解釈されます。 |
| skewY | <skewY()> | 数値はCSSの<angle>型としてdeg単位で解釈されます。 |
| matrix | <matrix()> |
SVG変形関数rotateの3値バージョンは、対応するCSS <transform-function>にマッピングできません。2つのオプションの数値は水平方向の変換値cxと垂直方向の変換値cyを表します。両方の数値はCSSの<length> 型としてpx単位で解釈され、回転の原点を定義します。この動作は、最初にcx, cyだけ移動し、最初の数値を<angle>型(deg単位)で解釈した回転を行い、その後-cx, -cyだけ移動するのと同等です。
transform属性はCSSトランジションの開始値または終了値になることができます。transform属性の値がCSSトランジションの開始値または終了値であり、SVGtransform listに3値のrotate変形関数が含まれている場合、個々のSVG変形関数をポストマルチプライして、その結果の行列を<matrix()>CSS <transform-function>としてCSSトランジションの開始値・終了値として使用する必要があります。
7.4. ユーザー座標空間
pattern
要素の場合、
patternTransform
属性およびtransformプロパティは、パターン座標系に追加の変形を定義します。詳細は
patternUnits
属性を参照してください [SVG2]。
linearGradient
および
radialGradient
要素の場合、
gradientTransform
属性およびtransformプロパティは、グラデーション座標系に追加の変形を定義します。詳細は
gradientUnits
属性を参照してください [SVG2]。
clipPath
要素の場合、transform属性およびtransformプロパティは、クリッピングパス座標空間に追加の変形を定義します。詳細は
clipPathUnits
属性を参照してください [CSS-MASKING]。
その他すべての変形可能要素では、transform属性およびtransformプロパティは、親の現在のユーザー座標系で変形を定義します。transform属性のすべてのパーセンテージ値は要素の基準ボックスに対する相対値です。
以下の例のパターンに対するtransform-originプロパティは、原点を水平方向・垂直方向それぞれ50%だけ移動させます。transformプロパティも絶対値で移動を指定しています。
<svg xmlns= "http://www.w3.org/2000/svg" >
<style>
pattern {
transform: rotate(45deg);
transform-origin: 50% 50%;
}
</style>
<defs>
<pattern id= "pattern-1" >
<rect id= "rect1" width= "100" height= "100" fill= "blue" />
</pattern>
</defs>
<rect width= "200" height= "200" fill= "url(#pattern-1)" />
</svg>
SVG
pattern
要素にはバウンディングボックスがありません。参照元の基準ボックスとして参照される
rect
要素の基準ボックスが、transform-originプロパティの相対値の解決に使われます。そのため、原点は一時的に100ピクセル移動し、pattern要素の内容のユーザー空間が回転されます。
7.5. SVG transform属性用DOMインターフェース
SVG仕様では、SVG DOMに"SVGAnimatedTransformList"
インターフェースを定義しており、SVGtransform、
gradientTransform
および
patternTransform
属性のアニメーション値および基準値にアクセスできます。後方互換性を維持するため、ユーザーエージェントはこのAPIを引き続きサポートしなければなりません。
baseValは、SVGtransform、
patternTransform、
gradientTransform
属性の値を取得・変更するための手段を著者に提供します。SVG DOMへの必要な後方互換性を提供するため、baseValはこの著者スタイルシートの値を反映しなければなりません。SVG DOMオブジェクトのbaseValの変更は、即座に著者スタイルシートに反映されなければなりません。
animValはtransformプロパティの算出スタイルを表します。したがって、適用されているCSS3トランジション、CSS3アニメーション、またはSVGアニメーションがあれば、それらすべてが含まれます。算出スタイルとSVG DOMのanimValオブジェクトは変更できません。
8. SVGアニメーション
8.1.
animate
要素および
set
要素
本仕様では、
animate
要素および
set
要素は、データ型<transform-list>をアニメーションできます。
アニメーション効果は、加算型
animate
アニメーション(下記参照)において基底値にポストマルチプライされます。これは<transform-list>アニメーション固有の挙動により、単に基底値に加算されるのではありません。
from-to、from-by、byアニメーションは、SMILで対応するvaluesアニメーションと等価と定義されています。ただし、toアニメーションは加算的・非加算的な挙動の混合です[SMIL3]。
animate
要素のtoアニメーションは、基底値からto属性値へのスムーズな変化を実現するための特有の機能を持ちます。しかしこれは加算型変形アニメーションがポストマルチプライされるべきという数学的要件と矛盾します。その結果、animate要素のtoアニメーションの挙動は未定義です。著者は任意の変形アニメーションを実現する際は、from-to、from-by、by、またはvaluesアニメーションの利用を推奨します。
データ型<transform-list>のアニメーションに対して、
calcMode属性の値"paced"は未定義です。
animate
要素で指定された場合、UAは"linear"値を選択しても構いません。今後の仕様では<transform-list>に対するpacedアニメーションの実装方法が定義される可能性があります。
注: 以下の段落はアニメーション可能な要素、属性、プロパティを拡張します[SVG11]。
導入された表示属性transform、
patternTransform、
gradientTransform
およびtransform-originはアニメーション可能です。
本仕様ではSVG基本データ型<transform-list>は、<transform-function>のリストと等価です。<transform-list>はアニメーション可能で加算的です。このデータ型はSVG
animate
要素およびSVG
set
要素でアニメーションできます。SVGアニメーションは、変形値間のトランジションとアニメーションで説明されているアニメーション手順と同じものを実行しなければなりません。
| データ型 | 加算可能か? |
animate
|
set
|
animateColor
|
animateTransform
| 備考 |
|---|---|---|---|---|---|---|
| <transform-list> | yes | yes | yes | no | yes |
animateTransform
での加算可能とは、変形が基底の変形集合にポストマルチプライされることを意味します。
|
8.2. 加算の中立要素
一部のアニメーションでは加算の中立要素が必要です。変形関数の場合、これは0のスカラーまたは0のスカラーのリストです。変形関数の中立要素の例:translate(0)、 scale(0)、rotate(0)、skewX(0)、skewY(0)です。
注: この段落は[SMIL]および[SVG11]による拡張の要件に焦点を当てています。本仕様では上記以外の変形関数の中立要素について定義していません。
byアニメーション(by値vbを持つ)は、値リストに加算の中立要素(ドメインの0)とvbを加えてadditive="sum"とした場合と等価です。[SMIL3]
<rect width= "100" height= "100" >
<animateTransform attributeName= "transform" attributeType= "XML"
type= "scale" by= "1" dur= "5s" fill= "freeze" />
</rect>
type="scale"のbyアニメーションで加算の中立要素は値0です。したがって上記アニメーションでは、0秒時点でrectは非表示(animated transform list値がscale(0))となり、5秒時点で元のサイズに戻ります(animated transform list値がscale(1))。
8.3. SVG 1.1 'attributeName'属性
SVG 1.1 Animationでは、対象属性の名前を指定するために"attributeName"属性を定義しています。表示属性
gradientTransform
および
patternTransform
では、値transformも指定できます。同じtransformプロパティがアニメーションされます。
この例では、線形グラデーションのグラデーション変形がアニメーションされます。
<linearGradient gradientTransform= "scale(2)" >
<animate attributeName= "gradientTransform" from= "scale(2)" to= "scale(4)"
dur= "3s" additive= "sum" />
<animate attributeName= "transform" from= "translate(0, 0)" to= "translate(100px, 100px)"
dur= "3s" additive= "sum" />
</linearGradient>
linearGradient
要素は
gradientTransform
表示属性を指定しています。2つの
animate
要素は、ターゲット属性
gradientTransform
とtransformを対象にしています。どちらも同じグラデーション変形に適用され、最初のアニメーションのスケールと次のアニメーションの移動が順に適用されます。
9. 変形関数
transformプロパティの値は、<transform-function>のリストです。 許可される変形関数の集合は下記に示します。 以下の関数では、 <zero>は0degと同様に動作します(単位なし0度角はレガシー互換のため保持)。 水平移動のパーセンテージは基準ボックスの幅に対する相対値です。 垂直移動のパーセンテージは基準ボックスの高さに対する相対値です。
9.1. 2D変形関数
- matrix() = matrix( <number> [, <number> ]{5,5} )
-
6つの値a, b, c, d, e, fによる変形行列として2D変形を指定します。
- translate() = translate( <length-percentage> [, <length-percentage> ]? )
-
ベクトル[tx, ty]による2D移動を指定します。txは最初のtranslation-valueパラメータ、tyは省略可能な2番目のtranslation-valueパラメータです。<ty>が指定されない場合、tyは0となります。
- translateX() = translateX( <length-percentage> )
-
指定量だけX方向に移動します。
- translateY() = translateY( <length-percentage> )
-
指定量だけY方向に移動します。
- scale() = scale( <number> [, <number> ]? )
-
[sx,sy]スケーリングベクトルで2Dスケール操作を指定します。2番目のパラメータが省略された場合、1番目の値と同じになります。例えば、scale(1, 1)は要素を変更しませんが、scale(2, 2)はX軸・Y軸とも2倍、面積は4倍になります。
- scaleX() = scaleX( <number> )
-
[sx,1]スケーリングベクトルで2Dスケール操作を指定します。sxがパラメータ値です。
- scaleY() = scaleY( <number> )
-
[1,sy]スケーリングベクトルで2Dスケール操作を指定します。syがパラメータ値です。
- rotate() = rotate( [ <angle> | <zero> ] )
-
指定された角度で、transform-originプロパティで定義された要素の原点を中心に2D回転を指定します。例えばrotate(90deg)は要素を時計回りに1/4回転させます。
- skew() = skew( [ <angle> | <zero> ] [, [ <angle> | <zero> ] ]? )
-
X・Y両軸の[ax,ay]による2Dスキューを指定します。2番目のパラメータが指定されない場合は0となります。
skew()は互換性維持のため存在しますが、新しいコンテンツでの使用は避けてください。代わりにskewX()やskewY()を使い、skew()の挙動がskewX()とskewY()の乗算と異なることに注意してください。
- skewX() = skewX( [ <angle> | <zero> ] )
-
指定された角度でX軸方向に2Dスキュー変換を指定します。
- skewY() = skewY( [ <angle> | <zero> ] )
-
指定された角度でY軸方向に2Dスキュー変換を指定します。
9.2. 変形関数の基本形と派生形
一部の変形関数は、より一般的な変形関数として表現できます。これらの関数は派生変形関数と呼ばれ、一般的な変形関数は基本変形関数と呼ばれます。2次元の基本形とその派生変形関数は次の通りです:
- translate()
- これは<translateX()>、<translateY()>、<translate()>のための基本形です。
- scale()
- これは<scaleX()>、<scaleY()>、<scale()>のための基本形です。
10. 変形関数リスト
複数の<transform-function>がリストとして指定された場合、すべての変形関数が指定された順に個別に適用された場合と同じ効果になります。
つまり、位置や寸法に影響を与える他のスタイルがない場合、入れ子のtransformは、祖先の座標系から要素のローカル座標系への一連の変形関数のリストを1つにまとめて適用するのと同等です。結果の変形はリスト内の変形の行列積になります。
< div style = "transform: translate(-10px, -20px) scale(2) rotate(45deg)" />
は、次のように機能的に同等です:
< div style = "transform: translate(-10px, -20px)" id = "root" >
< div style = "transform: scale(2)" >
< div style = "transform: rotate(45deg)" >
</ div >
</ div >
</ div >
変形関数によってオブジェクトの現在の変形行列が非可逆(invertibleでない)になる場合、そのオブジェクトおよび内容は表示されません。
次の例のオブジェクトはscale(0)で拡大縮小されます。
< style >
. box {
transform : scale( 0 );
}
</ style >
< div class = "box" >
Not visible
</ div >
このスケーリングにより、divボックスの座標空間のCTM(現在の変形行列)は非可逆となります。したがってdivボックスおよびその中のテキストは表示されません。
11. 変形の補間
補間は、以下のように変形関数リストに対して実施されます:
-
VaとVbの両方がnoneの場合:
-
Vresultはnoneになります。
-
-
noneは長さ0のリストとして扱われます。VaとVbの長さが異なる場合:
-
短い方のリストを長い方の長さまで拡張し、追加された各位置には、長い方のリストの対応する位置に合わせた単位変形関数を設定します。両方の変形関数リストは次の規則に従って補間されます。
-
-
Vresultを空リストとして用意します。
VaおよびVbの先頭から対応する関数同士を比較します:
-
関数が同じ名前、または同じ基本変形関数の派生であれば、§12 基本形・派生変形関数の補間に従って対応する関数ペアを補間し、結果をVresultに追加します。
-
ペアが共通の名前や基本変形関数を持たない場合、それぞれのVaとVbの残りの変形関数をポストマルチプライし、2つの4x4行列を生成します。これらの行列は補間され、§13 行列の補間の通りVresultに追加します。その後、VaとVbのイテレーションを終了します。
例えば、 Vaがrotate(0deg) scale(1) translate(20px)、Vbがrotate(270deg) translate(10px) scale(2)の場合、rotate(0deg)とrotate(360deg)は§12 基本形・派生変形関数の補間で補間され、残りのscale(1) translate(20px)とtranslate(10px) scale(2)はまず4x4行列に変換され、§13 行列の補間に従って補間されます。以前の仕様では、リスト内すべての関数が一致しない限り、ペアの補間を行いませんでした。そのため、この例ではマトリックス補間のみとなり、rotate(360deg)の成分は失われていました。
-
場合によっては、アニメーションによって変形行列が特異(singular)または非可逆になることがあります。例えば、scaleが1から-1に変化するアニメーションなど。このような状態になった時点で、変形された要素は描画されません。
12. 基本形・派生変形関数の補間
同じ名前で同じ引数数を持つ2つの変形関数は、変換なしで数値的に補間されます。計算された値は同じ変形関数タイプ・同じ引数数になります。<matrix()>には特別な規則が適用されます。
translate(0)とtranslate(100px)は同じ型で同じ引数数なので、数値的に補間できます。translateX(100px)は型が異なり、translate(100px, 0)は引数数が異なるため、これらは変換ステップなしで補間できません。
同じ基本形を共有する異なるタイプの変形関数、または同じタイプで引数数が異なる変形関数同士は補間可能です。両方ともまず共通の基本形に変換され、その後数値的に補間されます。計算された値は、補間後の引数で基本形になります。
次の例は、divボックスのホバー時にtranslateX(100px)からtranslateY(100px)への3秒のトランジションを示しています。両変形関数は同じ基本形translate()の派生なので補間できます。
div {
transform : translateX ( 100 px );
}
div:hover {
transform : translateY ( 100 px );
transition : transform 3 s ;
}
トランジション期間中、両変形関数は共通の基本形に変換されます。translateX(100px)はtranslate(100px, 0)に、translateY(100px)はtranslate(0, 100px)に変換され、両者とも数値的に補間されます。
両変形関数が2次元空間で共通の基本形を持つ場合は、両方とも2次元の基本形に変換されます。一方または両方が3次元変形関数の場合は、共通の3次元基本形が使われます。
この例では、2次元変形関数が3次元変形関数へアニメーションされます。共通の基本形はtranslate3d()です。
div {
transform : translateX ( 100 px );
}
div:hover {
transform : translateZ ( 100 px );
transition : transform 3 s ;
}
まずtranslateX(100px)はtranslate3d(100px, 0, 0)に、translateZ(100px)はtranslate3d(0, 0, 100px)に変換され、それぞれ数値的に補間されます。
13. 行列の補間
2つの行列を補間する際には、それぞれの行列を対応する移動、回転、スケール、スキューに分解します。分解された各成分同士を数値的に補間し、最後に再度行列として構成します。
< style >
div {
transform : rotate( 45 deg );
}
div : hover {
transform : translate( 100 px , 100 px ) rotate( 1215 deg );
transition : transform 3 s ;
}
</ style >
< div ></ div >
ソースtransformのrotate(45deg)と、ターゲットtransformのtranslate(100px, 100px) rotate(1125deg)は関数数が異なります。変形の補間の最後の規則によれば、両transformは行列補間で処理されます。変形関数を行列に変換することで、3回転の情報が失われ、要素は1/4回転(90°)しか回転しません。
上記例で3と1/4回転を実現するには、ソースおよびターゲットtransformが変形の補間の3つ目の規則を満たす必要があります。ソースtransformはtranslate(0, 0) rotate(45deg)のように関数数を揃えることで、線形補間が可能です。
以下では、2つの2D行列の補間と、少なくとも一方が2D行列でない場合の行列補間を区別します。
補間対象の行列が非可逆の場合、アニメーション関数は該当するアニメーション仕様の規則に従い、離散アニメーションにフォールバックする必要があります。
13.1. 補助関数
次のサブセクションの疑似コードでは、下記の補助関数を使用します:
Supporting functions (pointは3要素ベクトル、matrixは4x4行列、vectorは4要素ベクトルです):
double determinant(matrix) matrixの4x4行列式を返します
matrix inverse(matrix) 渡されたmatrixの逆行列を返します
matrix transpose(matrix) 渡されたmatrixの転置行列を返します
point multVecMatrix(point, matrix) 渡されたpointをmatrixで乗算し、変換後のpointを返します
double length(point) point(ベクトル)の長さを返します
point normalize(point) pointの長さを1に正規化します
double dot(point, point) 2つのpointのドット積を返します
double sqrt(double) 渡された値の平方根を返します
double max(double y, double x) 2つの値のうち大きい方を返します
double dot(vector, vector) 2つのvectorのドット積を返します
vector multVector(vector, vector) 2つのvectorを乗算します
double sqrt(double) 渡された値の平方根を返します
double max(double y, double x) 2つの値のうち大きい方を返します
double min(double y, double x) 2つの値のうち小さい方を返します
double cos(double) 渡された値のコサインを返します
double sin(double) 渡された値のサインを返します
double acos(double) 渡された値の逆コサインを返します
double abs(double) 渡された値の絶対値を返します
double rad2deg(double) ラジアン値を度に変換して返します
double deg2rad(double) 度をラジアン値に変換して返します
Decompositionでも下記関数を使用します:
point combine(point a, point b, double ascl, double bscl)
result[0] = (ascl * a[0]) + (bscl * b[0])
result[1] = (ascl * a[1]) + (bscl * b[1])
result[2] = (ascl * a[2]) + (bscl * b[2])
return result
13.2. 2D行列の補間
13.2.1. 2D行列の分解
以下の疑似コードは"Graphics Gems II, edited by Jim Arvo"の"unmatrix"手法に基づいています。
疑似コードの行列はカラム主順(column-major order)です。行列のインデックスの最初はカラム、2番目は行を表します。
Input: matrix ; 4x4行列
Output: translation ; 2要素ベクトル
scale ; 2要素ベクトル
angle ; 回転
m11 ; 2x2行列の1,1成分
m12 ; 2x2行列の1,2成分
m21 ; 2x2行列の2,1成分
m22 ; 2x2行列の2,2成分
Returns false if the matrix cannot be decomposed, true if it can
double row0x = matrix[0][0]
double row0y = matrix[0][1]
double row1x = matrix[1][0]
double row1y = matrix[1][1]
translate[0] = matrix[3][0]
translate[1] = matrix[3][1]
scale[0] = sqrt(row0x * row0x + row0y * row0y)
scale[1] = sqrt(row1x * row1x + row1y * row1y)
// 行列式が負の場合、いずれかの軸が反転している
double determinant = row0x * row1y - row0y * row1x
if (determinant < 0)
// 最小の単位ベクトルのドット積の軸を反転
if (row0x < row1y)
scale[0] = -scale[0]
else
scale[1] = -scale[1]
// スケール成分を除去するため正規化
if (scale[0])
row0x *= 1 / scale[0]
row0y *= 1 / scale[0]
if (scale[1])
row1x *= 1 / scale[1]
row1y *= 1 / scale[1]
// 回転を算出し、行列を正規化
angle = atan2(row0y, row0x);
if (angle)
// Rotate(-angle) = [cos(angle), sin(angle), -sin(angle), cos(angle)]
// = [row0x, -row0y, row0y, row0x]
// 上記の正規化のおかげで
double sn = -row0y
double cs = row0x
double m11 = row0x
double m12 = row0y
double m21 = row1x
double m22 = row1y
row0x = cs * m11 + sn * m21
row0y = cs * m12 + sn * m22
row1x = -sn * m11 + cs * m21
row1y = -sn * m12 + cs * m22
m11 = row0x
m12 = row0y
m21 = row1x
m22 = row1y
// 回転関数は度で扱うため変換
angle = rad2deg(angle)
return true
13.2.2. 分解した2D行列値の補間
2つの分解済み2D行列値を補間する前に、以下を実施します:
Input: translationA ; 2要素ベクトル
scaleA ; 2要素ベクトル
angleA ; 回転
m11A ; 2x2行列の1,1成分
m12A ; 2x2行列の1,2成分
m21A ; 2x2行列の2,1成分
m22A ; 2x2行列の2,2成分
translationB ; 2要素ベクトル
scaleB ; 2要素ベクトル
angleB ; 回転
m11B ; 2x2行列の1,1成分
m12B ; 2x2行列の1,2成分
m21B ; 2x2行列の2,1成分
m22B ; 2x2行列の2,2成分
// 一方のx軸と他方のy軸が反転している場合、非反転回転に変換
if ((scaleA[0] < 0 && scaleB[1] < 0) || (scaleA[1] < 0 && scaleB[0] < 0))
scaleA[0] = -scaleA[0]
scaleA[1] = -scaleA[1]
angleA += angleA < 0 ? 180 : -180
// 長い経路で回転しないようにする
if (!angleA)
angleA = 360
if (!angleB)
angleB = 360
if (abs(angleA - angleB) > 180)
if (angleA > angleB)
angleA -= 360
else
angleB -= 360
その後、ソース行列の分解値translation, scale, angle, m11~m22の各成分を、ターゲット行列の対応成分と線形補間します。
13.2.3. 2D行列への再構成
補間後、得られた値は要素のユーザー空間の変換に使われます。これらの値を再度4x4行列に構成する方法は、以下の疑似コードに従います。
行列はカラム主順(column-major order)です。インデックスの1つ目はカラム、2つ目は行です。
Input: translation ; 2要素ベクトル
scale ; 2要素ベクトル
angle ; 回転
m11 ; 2x2行列の1,1成分
m12 ; 2x2行列の1,2成分
m21 ; 2x2行列の2,1成分
m22 ; 2x2行列の2,2成分
Output: matrix ; identity初期化済み4x4行列
matrix[0][0] = m11
matrix[0][1] = m12
matrix[1][0] = m21
matrix[1][1] = m22
// 行列の移動
matrix[3][0] = translate[0] * m11 + translate[1] * m21
matrix[3][1] = translate[0] * m12 + translate[1] * m22
// 行列の回転
angle = deg2rad(angle);
double cosAngle = cos(angle);
double sinAngle = sin(angle);
// 一時的なidentity初期化済み4x4行列 rotateMatrix
rotateMatrix[0][0] = cosAngle
rotateMatrix[0][1] = sinAngle
rotateMatrix[1][0] = -sinAngle
rotateMatrix[1][1] = cosAngle
matrix = post-multiply(rotateMatrix, matrix)
// 行列のスケール
matrix[0][0] *= scale[0]
matrix[0][1] *= scale[0]
matrix[1][0] *= scale[1]
matrix[1][1] *= scale[1]
14. 変形関数の数学的記述
数学的には、すべての変形関数は次の形式の4x4変換行列として表現できます:
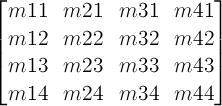
行列上の1単位の移動は、要素のローカル座標系で1ピクセルに相当します。
-
6つのパラメータa, b, c, d, e, fによる2D 3x2行列は、次の行列と等価です:

-
パラメータtxとtyによる2D移動は、tzが0値の3D移動と等価です。
-
パラメータsxとsyによる2Dスケールは、szが1値の3Dスケールと等価です。
-
パラメータalphaによる2D回転は、ベクトル[0,0,1]とパラメータalphaによる3D回転と等価です。
-
パラメータalphaとbetaによる2Dスキュー変形は、次の行列と等価です:
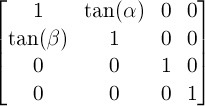
-
パラメータalphaによるX軸方向の2Dスキュー変形は、次の行列と等価です:
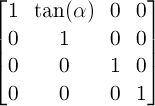
-
パラメータbetaによるY軸方向の2Dスキュー変形は、次の行列と等価です:
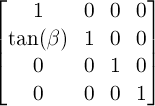
15. プライバシーとセキュリティの考慮事項
UAは、攻撃者が情報を推測したりタイミング攻撃を仕掛けたりできないように、変形操作を実装しなければなりません。タイミング攻撃とは、操作の実行時間を分析することで、本来保護されているコンテンツの情報を取得する手法です。
現時点では、この仕様固有の潜在的なプライバシーやセキュリティの懸念事項は報告されていません。
変更点
2018年11月30日作業草案からの変更点
-
実質的な変更なし
-
CR向けの雛形・スタイリング更新
2017年11月30日作業草案からの変更点
-
patternTransform、gradientTransform表示属性がtransformプロパティを表す仕様文を削除(SVG 2で指定予定)。
-
プライバシーとセキュリティセクション追加。
-
transform、
gradientTransformおよびpatternTransform属性の特別な構文追加。 -
疑似コードにおける行列要素のインデックス順序を明確化。
-
再構成疑似コードの乗算順序を明確化。
-
transformのオーバーフロー領域への影響を明確化。
-
中立要素リストからtranslateX(0)、translateY(0)、scaleX(0)、scaleY(0)を削除。
-
変形関数定義から3D変形に関する記述を削除。
-
変形リスト間の補間について、長さを揃え、共通接頭辞部分の行列補間を避けるように仕様化。
-
非置換インラインボックス、table-columnボックス、table-column-groupボックスにはtransformなしとする仕様化。
-
pattern、linearGradient、radialGradient、clipPath要素の変形のターゲット座標空間を定義。 -
変形関数の基本形から3値<rotate()>を削除。
-
ペイントサーバーおよび
clipPath要素の基準ボックスを定義。 -
3値rotateのtransform表示属性をトランジションの開始・終了値とした際の挙動を仕様化。
-
stroke-boxおよびcontent-boxをtransform-boxに追加。他仕様とのボックスマッピング挙動統一。
-
編集上の変更。
謝辞
編集者は、Robert O’Callahan、Cameron McCormack、Tab Atkins、Gérard Talbot、L. David Baron、Rik Cabanier、Brian Birtles、Benoit Jacob、Ken Shoemake、Alan Gresley、Maciej Stochowiak、Sylvain Galineau、Rafal Pietrak、Shane Stephens、Matt Rakow、XiangHongAi、Fabio M. Costa、Nivesh Rajbhandari、Rebecca Hauck、Gregg Tavares、Graham Clift、Erik Dahlström、Alexander Zolotov、Amelia Bellamy-Royds、Boris Zbarskyの慎重なレビュー、コメント、修正に感謝します。