1. はじめに
本仕様は、[css-transforms-1]を拡張するデルタ仕様であり、著者が要素を三次元空間で変形できるようにします。 transformプロパティ用の新しい変形関数は三次元変形を可能にし、 追加のプロパティによって三次元変形の扱いが容易になり、入れ子の三次元変形要素同士の相互作用を著者が制御できるようになります。
-
perspectiveプロパティは、子要素に追加のパースペクティブ変換を与えることができます。perspective-originプロパティは、パースペクティブが適用される原点を制御し、「消失点」の位置を効果的に変更します。
-
transform-styleプロパティは、3D変形された要素とその3D変形された子孫が共通の三次元空間を共有できるようにし、三次元オブジェクトの階層構造を構築できます。
-
backface-visibilityプロパティは、要素が三次元変形によって裏返され、裏面が表示される場合に関係します。この状況で要素を非表示にしたい場合は、このプロパティにhidden値を設定することで実現できます。
注: transformプロパティの一部の値は要素を三次元座標系で変形できますが、要素自体は三次元オブジェクトではありません。要素は二次元平面(フラットな面)上に存在し、奥行きはありません。
本仕様はさらに、scale、translate、rotateという3つの便利なプロパティも追加し、単純な変形の記述やアニメーションが容易になります。
1.1. モジュール間の相互作用
ここで定義される3D変形関数は、transformプロパティの関数セットを拡張します。
perspective、transform-style、backface-visibilityの一部の値は、すべての子孫の包含ブロックや積み重ねコンテキストの生成につながります。
三次元変形は要素の視覚的な重なり順に影響し、Appendix E([CSS21])で記述されている前後の描画順序を上書きします。
1.2. 値の定義
本仕様はCSSプロパティ定義規約([CSS21])に従い、値定義構文([CSS-VALUES-3])を使用します。 本仕様で定義されていない値型はCSS Values & Units [CSS-VALUES-3]で定義されます。他のCSSモジュールと組み合わせることでこれらの値型定義が拡張される場合があります。
各プロパティ定義に記載されたプロパティ固有の値に加え、 この仕様で定義されるすべてのプロパティはCSS全域キーワードもプロパティ値として受け付けます。 読みやすさのため、明示的な繰り返し記載はしていません。
2. 用語
- 3D変形要素
- 3D行列
-
4x4行列で、2D行列の要件を満たさないもの。
- 恒等変形関数
-
CSS Transformsの恒等変形関数に加え、恒等変形関数の例としては translate3d(0, 0, 0)、translateZ(0)、scaleZ(1)、rotate3d(1, 1, 1, 0)、rotateX(0)、rotateY(0)、rotateZ(0)、matrix3d(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1)などがあります。 特殊なケースとしてperspective: perspective(none)が挙げられます。 この場合、m34の値が極めて小さくなり、変形関数は恒等行列とみなされます。
- パースペクティブ行列
-
perspectiveおよびperspective-originプロパティの値から算出される行列(詳細は下記参照)。
- 累積3D変換行列
-
3Dレンダリングコンテキストのルートに対する要素ごとの行列(詳細は下記参照)。
- 3Dレンダリングコンテキスト
-
共通の三次元座標系を共有する共通の祖先を持つ要素群(詳細は下記参照)。
2.1. 算出値の<transform-list>のシリアライズ
<transform-list>(算出値)は、下記アルゴリズムにより<matrix()>または<matrix3d()>関数のいずれかとしてシリアライズされます:
-
transformを恒等行列で初期化した4x4行列とする。transformの要素m11、m22、m33、m44は1に、その他は0に設定する。
-
<transform-function>を<transform-list>内で全て後置乗算でtransformに適用する。
-
<matrix()>または<matrix3d()>のどちらでシリアライズするか選択:
- transformが2D行列の場合
- transformを<matrix()>関数としてシリアライズする。
- それ以外の場合
- transformを<matrix3d()>関数としてシリアライズする。
この文言はCSS Transforms 1の本文に追加するよう修正が必要です。
3. 二次元サブセット
UAは常に三次元変形をレンダリングできるとは限らず、そうした場合は本仕様の二次元サブセットのみをサポートします。この場合、三次元変形やtransform-style、perspective、perspective-origin、backface-visibilityはサポートされません。Section 3D変形レンダリングは適用されません。行列分解は「Graphics Gems II, edited by Jim Arvo」の"unmatrix"メソッドから技術を使い、2D用に簡略化しています。Section 変形関数の数学的記述は引き続き有効ですが、a=m11、b=m12、c=m21、d=m22、e=m41、f=m42(2Dの3x2行列、6パラメーター)を使った3x3変換行列に簡略化できます。
二次元変形用の3x3行列。
著者はUAが三次元変形をサポートしない場合も容易にフォールバックを指定できます。次の例ではtransformプロパティが2つ定義されています。最初は2つの二次元変形関数のみ、2番目は二次元と三次元の変形関数が混在しています。
div { transform: scale(2) rotate(45deg);
transform: scale(2) rotate3d(0, 0, 1, 45deg);
}
3Dサポートがある場合は2番目の定義が最初の定義を上書きします。3Dサポートがない場合は2番目の定義が無効となり、UAは最初の定義にフォールバックします。
4. 変形レンダリングモデル
この仕様は CSS Transforms 1 § 3 変形レンダリングモデル を拡張し、三次元変形関数の存在、transform-origin のZ値、perspectiveプロパティ、そして transform-style プロパティの使用値が preserve-3d の場合に適用される新しい3Dレンダリングモデルに対応しています。
三次元変形関数は概念的に座標空間を三次元に拡張し、スクリーンの平面に垂直なZ軸を追加します。Z軸は画面奥から手前(ユーザー側)に向かって増加します。

座標空間の初期状態のデモ。
3D変形では transform-origin のZ成分が結果に影響するため、変換行列は transform と transform-origin プロパティから以下の手順で計算されます:
-
恒等行列で開始する。
-
transform-origin の算出X,Y,Zで平行移動する
-
transform プロパティの変形関数それぞれを左から右へ乗算する
-
transform-origin の算出X,Y,Zの負値で平行移動する
4.1. 3D変形レンダリング
通常、要素は平面としてレンダリングされ、積み重ねコンテキストと同じ平面に描画されます。しばしばこれはページ全体が共有する平面です。二次元変形関数は要素の見た目を変えることができますが、その要素は依然として積み重ねコンテキストと同じ平面に描画されます。
三次元変形を持つ要素が 3Dレンダリングコンテキスト に含まれていない場合、適切な変形が適用された状態で描画されますが、他の要素と交差しません。この場合の三次元変形は二次元変形と同様に単なるペインティング効果とみなせます。同様に、変形は描画順序に影響しません。例えば、Z方向に正の値で平行移動した変形は要素を大きく見せますが、その要素がZ変換なしの要素の前面に描画されることはありません。
入れ子の3D変形要素のレンダリング方法(数式含む?)を記述すること
この例は三次元変形が要素に適用された場合の効果を示します。
<style>
div {
height: 150px;
width: 150px;
}
.container {
border: 1px solid black;
}
.transformed {
transform: rotateY(50deg);
}
</style>
<div class="container">
<div class="transformed"></div>
</div>

変形は垂直(Y軸)周りに50度回転です。青いボックスが細く見える点に注目してください。ただし三次元的には見えません。
4.1.1. パースペクティブ
パースペクティブを使うことで、Z軸上で高い(ユーザーに近い)要素ほど大きく、遠いものほど小さく描画され、奥行き感を演出できます。拡大率は d/(d − Z) で、dは perspective プロパティ値、すなわち描画面から視点の距離です。
パースペクティブの効果は3D変形要素に2通りで適用できます。1つ目は、要素の 'transform function list' に perspective() 関数を含めることで、要素の 'current transformation matrix' に計算されます。
2つ目は、perspective と perspective-origin プロパティを要素に適用して、その3D変形された子要素の描画に影響を与え、同じ三次元シーンに存在するような印象を与えるパースペクティブを共有させます。

perspectiveプロパティとZ位置によるスケーリングの違いを示す図。上の図ではZがdの半分。元の円(実線)がZ(破線円)位置に表示されるようにするため、円が2倍に拡大されて水色円になる。下の図では円が1/3に縮小されて元の位置より奥に表示される。
通常、視点の位置は描画の中心にあります。この位置は、例えば複数の描画が同じパースペクティブを共有すべき場合など、perspective-originを設定することで変更できます。
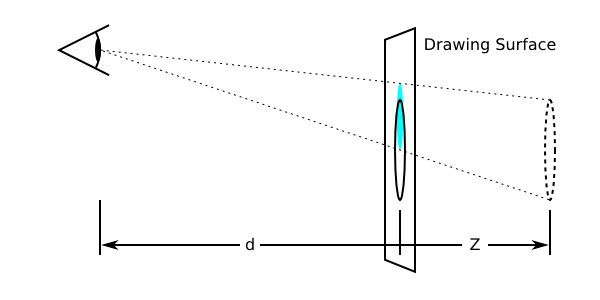
perspective-originを上方に動かした効果の図。
パースペクティブ行列は次のように計算されます:
-
恒等行列で開始。
-
perspective-originの算出X,Yで平行移動。
-
perspective()変形関数から得られる行列を、perspectiveプロパティの値を長さとして乗算する。
-
perspective-originの算出X,Yの負値で平行移動。
この例は、パースペクティブを使うことで三次元変形がより現実的に見えることを示します。
<style>
div {
height: 150px;
width: 150px;
}
.container {
perspective: 500px;
border: 1px solid black;
}
.transformed {
transform: rotateY(50deg);
}
</style>
<div class="container">
<div class="transformed"></div>
</div>

内側の要素は前の例と同じ変形ですが、今回は親要素のperspectiveプロパティによってレンダリングが影響されます。perspectiveはZ座標が正(ユーザーに近い)頂点のX,Yを拡大し、奥(負のZ座標)は縮小することで奥行き感を生みます。
4.1.2. 3Dレンダリングコンテキスト
このセクションでは、3D変形と transform-style プロパティを使ったコンテンツのレンダリングモデルを定義します。このモデルを説明するため、「3Dレンダリングコンテキスト」という概念を導入します。
3Dレンダリングコンテキストは、共通の祖先を持つ要素群であり、3D変形レンダリングの目的で共通の三次元座標系を共有するとみなされます。3Dレンダリングコンテキスト内の要素の前後順は三次元空間でのz位置に依存し、3D変形によって要素同士が交差する場合は交差して描画されます。
その三次元空間内の各要素の位置は、指定された要素から 変換行列を累積し、3Dレンダリングコンテキストを確立する要素まで辿ることで決定されます。
要素は次のように3Dレンダリングコンテキストを確立または参加します:
-
3Dレンダリングコンテキストは、使用値が preserve-3d かつ自身が別の3Dレンダリングコンテキストに属していない 変形可能要素によって確立されます。確立した要素自身もそのコンテキストに参加します。
-
使用値が preserve-3d かつ既に 3Dレンダリングコンテキストに参加している要素は、新たなコンテキストを作らず、既存のコンテキストを拡張します。
-
親要素が3Dレンダリングコンテキストを確立または拡張している場合、その子要素は 3Dレンダリングコンテキストに参加します。
一部のCSSプロパティは「グループ化」を強制する値があり、要素とその子孫を他の要素と合成する前にグループとして描画させます。これにはopacityやfilter、クリッピングに関わるプロパティなどが含まれます。該当プロパティ値は グループ化プロパティ値 で示されています。これらをtransform-style:preserve-3dな要素で使用すると、使用値は flat となり、3Dレンダリングコンテキストの確立や拡張ができなくなります。
3Dレンダリングコンテキスト内では、要素の描画・ソートは次のように行われます:
-
3Dレンダリングコンテキストを確立する要素と、そのコンテキストに参加する他の3D変形要素はそれぞれ自身の平面に描画されます。この平面には、要素の背景、枠線、その他装飾、内容、および子孫要素が含まれます。ただし自身の平面を持つ子孫(およびその子孫)は除きます。描画は CSS 2.1, Appendix E, Section E.2 ペインティング順序に従います。
-
これらの平面群の間で交差判定を行い、Newellのアルゴリズムによって、累積3D変換行列で変換された平面で判定します。同じ平面(コープレーナー)の3D変形要素はペインティング順で描画されます。
注: この仕様では以前、確立要素の背景・枠線などの装飾が3Dシーン全体の背後に描画されると定義していましたが、#6238で変更されました。今後3Dレンダリングコンテキストの定義が変更された場合は元に戻す検討もありえます。
なお、変形で負のz成分を持つ要素は、確立要素のコンテンツや未変形の子孫の背後に描画され、3D変形要素は未変形要素や内容と相互に貫通する場合があります。
注: 3Dレンダリングコンテキスト内の3D変形要素はすべて奥行き順でソート・交差するため、兄弟のように描画されます。transform-style: preserve-3dの効果は、3Dレンダリングコンテキスト内の3D変形要素を確立要素まで持ち上げて描画するが、累積3D変換行列で変形したまま描画される、というイメージです。
<style>
div {
height: 150px;
width: 150px;
}
.scene {
background-color: rgba(0, 0, 0, 0.3);
border: 1px solid black;
perspective: 500px;
}
.container {
transform-style: preserve-3d;
}
.container > div {
position: absolute;
left: 0;
}
.container > :first-child {
transform: rotateY(45deg);
background-color: orange;
top: 10px;
height: 135px;
}
.container > :last-child {
transform: translateZ(40px);
background-color: rgba(0, 0, 255, 0.6);
top: 50px;
height: 100px;
}
</style>
<div class="scene">
<div class="container">
Lorem ipsum dolor sit amet, consectetaur adipisicing elit…
<div></div>
<div></div>
</div>
</div>
この例は、3Dレンダリングコンテキスト内で要素同士が交差できることを示しています。container要素は自身とその2つの子要素のために3Dレンダリングコンテキストを確立し、scene要素はそのコンテキストにパースペクティブを追加します。子要素同士が交差し、オレンジ色の要素はcontainerとも交差します。

<style>
div {
height: 150px;
width: 150px;
}
.container {
perspective: 500px;
border: 1px solid black;
}
.transformed {
transform: rotateY(50deg);
background-color: blue;
}
.child {
transform-origin: top left;
transform: rotateX(40deg);
background-color: lime;
}
</style>
<div class="container">
<div class="transformed">
<div class="child"></div>
</div>
</div>
この例は入れ子の3D変形のレンダリングを示します。青いdivは前の例と同じ変形で、親要素のperspectiveで描画が影響されます。ライム色要素もX軸回転(transform-originで上端固定)で3D変形されていますが、ライム要素は親の平面に描画されており、同じ3Dレンダリングコンテキストには属していません。そのためライム要素は短くなるだけで、青い要素から「飛び出して」見えることはありません。
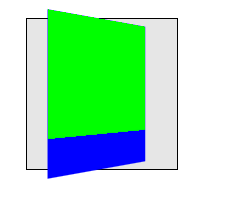
4.1.3. 変形要素の階層構造
デフォルトでは、変形要素は 3Dレンダリングコンテキスト を作らず、内容を平坦化して描画します。しかし、共通の三次元空間を共有する変形オブジェクトの階層構造を作るのは有用なため、transform-style プロパティに preserve-3d を指定すればこの平坦化挙動を上書きできます。これにより、変形要素の子孫も同じ3Dレンダリングコンテキストを共有できます。そうした要素の非3D変形子孫は前述Cのステップで要素の平面に描画されますが、同じ3Dレンダリングコンテキストの3D変形要素は独自の平面に「飛び出して」描画されます。
<style>
div {
height: 150px;
width: 150px;
}
.container {
perspective: 500px;
border: 1px solid black;
}
.transformed {
transform-style: preserve-3d;
transform: rotateY(50deg);
background-color: blue;
}
.child {
transform-origin: top left;
transform: rotateX(40deg);
background-color: lime;
}
</style>
この例は前の例と同じですが、青い要素に transform-style: preserve-3d が追加されています。青い要素はcontainerの3Dレンダリングコンテキストを拡張します。これで青・ライム両方の要素が共通の三次元空間を共有し、ライム要素が親から傾いて飛び出すように描画され、containerのperspectiveの影響も受けます。
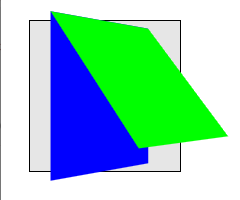
4.1.4. 累積3D変換行列の計算
要素を3Dレンダリングコンテキストでレンダリングする際に使用される最終的なtransform値は、以下の手順で累積3D変換行列を計算することで得られます:
-
transformを恒等行列とする。
-
current elementを変形された要素とする。
-
parent elementを変形された要素の親要素とする。
-
current elementが変形された要素の3Dレンダリングコンテキスト内の要素である間、以下を繰り返す:
-
current elementのtransform値がnoneでない場合、current elementの変換行列をtransformに前乗算する。
-
current elementがparent elementからのオフセット(スクロールオフセット含む)を表す平行移動行列を計算し、それをtransformに前乗算する。
-
parent elementのperspective値がnoneでない場合、parent elementのパースペクティブ行列をtransformに前乗算する。
-
current elementをparent elementとする。
-
parent elementをcurrent elementの親要素とする。
-
注: ここで述べるように、累積3D変換行列は、変形された要素やその祖先チェーンにおいて視覚フォーマットモデルによって発生するオフセット(スクロールオフセット含む)を考慮します。これは、その要素が属する3Dレンダリングコンテキストを確立する要素まで含めて処理されます。
4.1.5. 裏面の可視性
三次元変形を使うことで、要素の裏側が見えるように変形することができます。3D変形された要素は両面に同じ内容を表示するため、裏面は表面の鏡像のように見えます(要素がガラス板に投影されたかのよう)。通常、裏面がユーザー側になる場合も要素は表示されたままです。しかし、backface-visibilityプロパティを使うことで、裏面がユーザー側に来た時に要素を不可視にすることができます。この挙動は「ライブ」であり、backface-visibility: hiddenを指定した要素がアニメーションして表裏が交互に表示される場合、表面がユーザー側に来ている時だけ可視となります。
要素の裏面可視性は累積3D変換行列で判定されるため、3Dレンダリングコンテキストを確立する要素の親に対して相対的に判断されます。
注: このプロパティは、例えば2つの要素を背中合わせに配置してトランプカードを作る場合に便利です。このプロパティがないと、アニメーションでカードをひっくり返す際に前面・背面要素が入れ替わることがあります。6つの要素で箱を作る場合、内側の面だけを表示したい場合にも有用です。
この例は、クリックで裏返る「カード」要素の作り方を示します。#cardの"transform-style: preserve-3d"指定に注目してください。これは裏返した時に平坦化されるのを防ぐために必要です。
<style>
.body { perspective: 500px; }
#card {
position: relative;
height: 300px; width: 200px;
transition: transform 1s;
transform-style: preserve-3d;
}
#card.flipped {
transform: rotateY(180deg);
}
.face {
position: absolute;
top: 0; left: 0;
width: 100%; height: 100%;
background-color: silver;
border-radius: 40px;
backface-visibility: hidden;
}
.back {
transform: rotateY(180deg);
}
</style>
<div id="card" onclick="this.classList.toggle('flipped')">
<div class="front face">Front</div>
<div class="back face">Back</div>
</div>
backface-visibilityが非変形要素や2D変形要素に与える影響は?独自の平面に分離されて交差するのか?
4.2. パースペクティブ変形ボックスの処理
これは、与えられた行列を使って要素を厳密にどう変形するかを仕様化しようとする最初の試みです。理想的ではないかもしれませんので、実装者からのフィードバックを歓迎します。#912も参照。
累積3D変換行列は、perspectiveプロパティと、transformプロパティに含まれるperspective()変形関数の両方の影響を受けます。
この累積3D変換行列は4×4行列ですが、変形対象は二次元ボックスです。ボックスの各コーナー(a, b)を変形するには、まず(a, b, 0, 1)に行列を適用し、結果として4次元点(x, y, z, w)を得ます。これを以下のように3次元点(x′, y′, z′)に変換します:
w > 0 の場合、(x′, y′, z′) = (x/w, y/w, z/w)。
w = 0 の場合、(x′, y′, z′) = (x ⋅ n, y ⋅ n, z ⋅ n)。nは実装依存の値であり、可能ならx′やy′がビューポートサイズより十分大きくなる値を選ぶべきです。例えば、(5px, 22px, 0px, 0)は(5000px, 22000px, 0px)になるようn=1000など。ただし(0.1px, 0.05px, 0px, 0)にはこのnは小さすぎます。本仕様ではnの値は厳密には定めません。概念的には(x′, y′, z′)は(x, y, z)方向に無限遠です。
変形後のボックスの4つのコーナー全てでw < 0の場合、そのボックスは描画されません。
変形後のボックスのコーナーのうち1〜3個がw < 0の場合、その部分を切り取った多角形に置き換える必要があります。一般的には頂点が3〜5個の多角形となり、ちょうど2つがw = 0、残りはw > 0になります。これらの頂点は前述の規則で3次元点に変換されます。概念的にはw < 0の点は「視点の背後」なので表示すべきではありません。
.transformed {
height: 100px;
width: 100px;
background: lime;
transform: perspective(50px) translateZ(100px);
}
このボックスの全てのコーナーのz座標がperspectiveより大きくなります。つまりボックスは視点の背後となり、表示されません。数学的には、点(x, y)はまず(x, y, 0, 1)となり、(100px)平行移動で(x, y, 100, 1)となり、perspective適用で(x, y, 100, −1)となります。w座標が負なので表示されません。w < 0のケースを特別扱いしない実装の場合、(−x, −y, −100)として描画され、ボックスが左右反転することになります。
.transformed {
height: 100px;
width: 100px;
background: radial-gradient(yellow, blue);
transform: perspective(50px) translateZ(50px);
}
この場合、ボックスは視点位置まで移動されます。これはボックスを視点にどんどん近づけて、視野全体を埋めるようなものです。デフォルトのtransform-originはボックスの中心(黄色)なので、画面全体が黄色に覆われます。
数学的には、(x, y)はまず(x, y, 0, 1)となり、(50px)平行移動で(x, y, 50, 1)、perspective適用後は(x, y, 50, 0)となります。中心がtransform-originの場合、左上隅は(−50, −50)なので(−50, −50, 50, 0)となり、非常に左上遠く(例:−5000, −5000, 5000)に変換されます。他のコーナーも同様に遠くへ。ラジアルグラデーションはボックス全体に引き伸ばされ、可視部分は中心ピクセル(黄色)となります。ただしボックスは無限大ではないので、ユーザーはスクロールで青い部分も見ることができます。
.transformed {
height: 50px;
width: 50px;
background: lime;
border: 25px solid blue;
transform-origin: left;
transform: perspective(50px) rotateY(-45deg);
}
ボックスはユーザー側に向けて回転し、左端は固定され、右端が手前に動きます。右端はz = 70.7px付近となり、perspective 50pxより近くなります。そのため右端は消失し(視点の背後)、残りの部分は右方向に無限遠まで伸びます。
数学的には、右上頂点はtransform-originから見て(100, −50)。これを(x, y, 0, 1)に拡張し、変形後はおよそ(70.71, −50, 70.71, −0.4142)となります。w = −0.4142 < 0なので、w < 0部分を切り取る必要があります。新しい右上頂点は(50, −50, 50, 0)となり、さらに遠く(例:5000, −5000, 5000)に変換されます。他のコーナーも同様。結果としてボックスは画面右端を大きく超えて伸びます。
レンダリングされるボックスは有限なので、ユーザーはスクロールで全体を見ることができますが、右端約30pxは表示されません。青い枠は25px幅なので、左・上・下には表示されますが右端には出ません。
1つまたは3つの頂点がw < 0の場合でも同様の手順で処理され、切り取った結果が三角形や五角形になることもあります。
5. 個別変形プロパティ:translate、scale、rotateプロパティ
translate、rotate、scaleプロパティは、 著者が単純な変形を個別に指定できるようにします。 これは一般的なユーザーインターフェースの使い方に合った方法であり、 transformで translate()、 rotate()、 scale()の順序を覚えておく必要なく、 それらを独立して画面座標上で動作させることができます。
| 名前: | translate |
|---|---|
| 値: | none | <length-percentage> [ <length-percentage> <length>? ]? |
| 初期値: | none |
| 適用対象: | 変形可能要素 |
| 継承: | no |
| パーセンテージ: | (最初の値は)reference boxの幅、(2番目は)高さに対して相対 |
| 算出値: | キーワードnoneまたは算出済み<length-percentage>2つと絶対長さのペア |
| 正規順序: | 文法に従う |
| アニメーション型: | 算出値で、ただしnoneは下記参照 |
translateプロパティは1~3個の値を受け付け、 それぞれX、Y、Z軸での移動量を指定します。 2番目と3番目の値が省略された場合、 デフォルトは0pxです。
3番目の値が省略または0の場合、 これは2次元の移動指定となり、 translate()関数と等価です。 それ以外の場合、 これは3次元の移動指定となり、 translate3d()関数と等価です。
注: 解決値としてのtranslateプロパティは
算出値であり、
getComputedStyle()
の結果にはパーセンテージ値も含まれます。
| 名前: | rotate |
|---|---|
| 値: | none | <angle> | [ x | y | z | <number>{3} ] && <angle> |
| 初期値: | none |
| 適用対象: | 変形可能要素 |
| 継承: | no |
| パーセンテージ: | 該当なし |
| 算出値: | キーワードnone、または<angle>と軸(三つの<number>のリスト) |
| 正規順序: | 文法に従う |
| アニメーション型: | SLERPで、ただしnoneは下記参照 |
rotateプロパティは、 要素を回転させる角度と、 オプションで回転軸を受け付けます。
軸はx、 y、 またはzキーワードで指定でき、 その軸周りに回転します。 これはrotateX()、 rotateY()、 rotateZ() 変形関数と等価です。 また、軸は原点中心のベクトル(x,y,z成分の三つの数値)で明示的に指定することもでき、 rotate3d()関数と等価です。
単なる<angle>指定と、 z軸周り(zキーワードや x,y成分が0でz成分が正のベクトル指定)の回転の間に挙動の差はありません。 いずれもrotate()関数と等価な2D回転です。 例えば、rotate: 30deg、rotate: z 30deg、rotate: 0 0 1 30degは全て同じ意味です。
| 名前: | scale |
|---|---|
| 値: | none | [ <number> | <percentage> ]{1,3} |
| 初期値: | none |
| 適用対象: | 変形可能要素 |
| 継承: | no |
| パーセンテージ: | 該当なし |
| 算出値: | キーワードnone、または3つの<number>リスト |
| 正規順序: | 文法に従う |
| アニメーション型: | 算出値で、ただしnoneは下記参照 |
scale プロパティは1~3個の値を受け付け、 それぞれX、Y、Z軸の拡大率を指定します。
Y値が指定されない場合、 X値と同じになります。
Z値が指定されない場合、 デフォルトは1です。
3番目の値が省略、1、100%のいずれかの場合、 これは2次元の拡大指定で、 scale()関数と等価です。 それ以外の場合は 3次元の拡大指定となり、 scale3d()関数と等価です。
3番目の値が省略でも、1や100%でも挙動に違いはありません。
<percentage>は<number>と等価です。 例えばscale: 100%はscale: 1と等価です。 シリアライズ時は数値が使われます。
3つのプロパティはいずれも (初期値としても) none を受け付け、 これは変形を全く行いません。 特にこの値は 積み重ねコンテキストやすべての子孫の包含ブロックを作りませんが、 それ以外の値 (translate: 0pxのような「恒等」変形も含む)は 通常通り積み重ねコンテキストやすべての子孫の包含ブロックを作ります。
translate、rotate、scaleがアニメートやトランジションしていて、from値またはto値(両方でない)がnoneの場合、noneは同等の恒等値(translateは0px、rotateは0deg、scaleは1)に置き換えられます。
5.1. シリアライズ
これらのプロパティは、「変形なし」と「変形あり」という2つの異なる挙動モードがあるため、 シリアライズ時はその点を考慮する必要があります:
- translateの場合
-
移動が指定されている場合、 プロパティは1個〜3個の値でシリアライズされます。 (通常通り、2番目と3番目の値が0px(デフォルト)なら、あるいは3番目だけが0pxなら、 それらの0px値はシリアライズ時に省略します)。
元々noneが指定されていた場合に限り、キーワードnoneとしてシリアライズされなければなりません。 (単位変形は対象外です;その場合は0pxとしてシリアライズされなければなりません。)
- rotateの場合
-
z軸周り(2D)の回転が指定されている場合、 プロパティは<angle>のみでシリアライズされます。
その他の回転が指定された場合、 軸も含めてシリアライズされます。 軸がxまたはyと平行な場合は、該当キーワードでシリアライズされます。
元々noneが指定されていた場合に限り、キーワードnoneとしてシリアライズされなければなりません。 (単位変形は対象外です;その場合は0degとしてシリアライズされなければなりません。)
- scaleの場合
-
拡大率が指定されている場合、 プロパティは1個〜3個の値だけでシリアライズされます。 通常通り、3番目の値が1(デフォルト)なら、シリアライズ時に省略します。 3番目が省略され、かつ2番目が1番目と同じ(デフォルト)なら、2番目もシリアライズ時に省略します。
元々noneが指定されていた場合に限り、キーワードnoneとしてシリアライズされなければなりません。 (単位変形は対象外です;その場合は1としてシリアライズされなければなりません。)
6. 現在の変換行列
変換行列の計算手順は以下の通り修正されます:
変換行列は、transform、 transform-origin、translate、rotate、scale、offsetプロパティから次のように計算されます:
-
恒等行列で開始する。
-
transform-originの算出X、Y、Zで平行移動する。
-
translateの算出X、Y、Zで平行移動する。
-
scaleの算出X、Y、Zで拡大する。
-
offsetで指定した変形で平行移動・回転する。
-
transform内の変形関数を左から右に乗算する。
-
transform-originの算出X、Y、Zの負値で平行移動する。
7. transform-styleプロパティ
| 名前: | transform-style |
|---|---|
| 値: | flat | preserve-3d |
| 初期値: | flat |
| 適用対象: | 変形可能要素 |
| 継承: | no |
| パーセンテージ: | N/A |
| 算出値: | 指定キーワード |
| 正規順序: | 文法に従う |
| アニメーション型: | 離散 |
| 使用値: | グループ化プロパティが存在する場合はflat、それ以外は指定キーワード |
transform-styleがpreserve-3dとなった変形可能要素は、積み重ねコンテキストとすべての子孫の包含ブロックを両方確立します。 使用値がpreserve-3dの場合、3Dレンダリングコンテキストも確立または拡張します。
7.1. グループ化プロパティ値
次のCSSプロパティ値は、子孫要素を平坦化して描画した後でないと適用できないため、preserve-3dでも使用値をflatに強制します。
-
opacity: 1未満の値。
-
filter: none以外の値。
-
clip-path: none以外の値。
-
isolation: 使用値がisolate。
-
mask-image: none以外の値。
-
mask-border-source: none以外の値。
-
mix-blend-mode: normal以外の値。
-
contain: paint およびペイント包含となるその他のプロパティ値の組み合わせ。注: これには使用値に影響する他のプロパティ(例:content-visibility: hidden)も含まれます。
8. perspectiveプロパティ
| 名前: | perspective |
|---|---|
| 値: | none | <length [0,∞]> |
| 初期値: | none |
| 適用対象: | 変形可能要素 |
| 継承: | no |
| パーセンテージ: | N/A |
| 算出値: | キーワードnoneまたは絶対長さ |
| 正規順序: | 文法に従う |
| アニメーション型: | 算出値で |
- <length [0,∞]>
-
投影中心までの距離。
非常に小さい<length> 値は奇妙な描画結果や変形計算の精度問題を引き起こすため、 1px未満の値はレンダリング上は1pxとして扱う必要があります。 (この制限は値そのものには影響せず、 スタイルシート内でperspective: 0;と指定しても シリアライズ時は0となります。)
- none
-
パースペクティブ変形は適用されません。効果は数学的には無限大<length> 値と同様です。すべてのオブジェクトはキャンバス上で平坦に見えます。
このプロパティをnone以外で使うと積み重ねコンテキストが確立されます。 また、すべての子孫の包含ブロックも確立されます(transformプロパティと同様)。
perspectiveで積み重ねコンテキスト・包含ブロックが必要かは微妙だが、Web互換性のため変更できないかも。
perspectiveおよびperspective-originの値は、上述の通りパースペクティブ行列の計算に使用されます。
9. perspective-originプロパティ
perspective-originプロパティはperspectiveプロパティの原点を定義します。これは、要素の子に対して、視点(X・Y座標)がどこにあるかを設定するものです。
| 名前: | perspective-origin |
|---|---|
| 値: | <position> |
| 初期値: | 50% 50% |
| 適用対象: | 変形可能要素 |
| 継承: | no |
| パーセンテージ: | reference boxのサイズを参照 |
| 算出値: | background-positionを参照 |
| 正規順序: | 文法どおり |
| アニメーション型: | 算出値による |
perspectiveとperspective-originの値は、上記で述べたパースペクティブ行列の計算に使われます。
perspective-originの値は、reference boxの左上隅からのオフセットを表します。
- <percentage>
-
水平方向のパーセンテージはreference boxの幅に対し、垂直方向のパーセンテージはreference boxの高さに対して相対です。水平・垂直の値は共に、reference boxの左上隅からのオフセットを表します。
- <length>
-
長さ値は固定長のオフセットを与えます。水平・垂直ともに、reference boxの左上隅からのオフセットです。
- top
-
1つまたは2つ値が指定された場合、垂直位置は0%となり、それ以外の場合は次のオフセットの基準が上端となります。
- right
-
1つまたは2つ値が指定された場合、水平方向は100%となり、それ以外の場合は次のオフセットの基準が右端となります。
- bottom
-
1つまたは2つ値が指定された場合、垂直方向は100%となり、それ以外の場合は次のオフセットの基準が下端となります。
- left
-
1つまたは2つ値が指定された場合、水平方向は0%となり、それ以外の場合は次のオフセットの基準が左端となります。
- center
-
水平方向が指定されていない場合は50%(left 50%)、垂直方向が指定されていれば50%(top 50%)となります。
perspective-originプロパティはheightと同じく解決値の特別扱いプロパティです。[CSSOM]
10. backface-visibilityプロパティ
| 名前: | backface-visibility |
|---|---|
| 値: | visible | hidden |
| 初期値: | visible |
| 適用対象: | 変形可能要素 |
| 継承: | no |
| パーセンテージ: | N/A |
| 算出値: | 指定キーワード |
| 正規順序: | 文法どおり |
| アニメーション型: | 離散 |
backface-visibility: hiddenが指定された要素の可視性は、次のように判定されます:
-
要素の累積3D変換行列を計算する。
-
行列の3行3列目の成分が負の場合、その要素は非表示にする。そうでなければ表示する。
backface-visibilityはm33だけでは判定できません。#917参照。
注: この定義の理由は以下です。要素は厚みが無視できる長方形と仮定します。未変形状態の前面は(x, y, ε)、背面は(x, y, −ε)です(εは非常に小さい値)。変形後、前面がユーザー側(z値大)か背面がユーザー側かを判定します。前面のz座標は m13x + m23y + m33ε + m43、背面は m13x + m23y − m33ε + m43です。前者が後者より大きいのは m33 > 0 のときのみです(0の場合は前面・背面が等距離で、たとえば90度回転で不可視となるので気にしなくてよい)。
11. SVGと3D変形関数
本仕様では、三次元変形関数が以下のコンテナ要素に適用されることを明示的に要求します:
a,
g,
svg,
すべてのグラフィック要素、すべてのグラフィック参照要素、SVGの
foreignObject
要素。
三次元変形関数と、perspective、perspective-origin、transform-style、backface-visibilityは、以下の要素では使用できません:
clipPath,
linearGradient,
radialGradient
および
pattern。
変形リストに三次元変形関数が含まれている場合、変形リスト全体は無視されます。これらのプロパティ値もすべて無視されます。これらの要素に含まれる変形可能要素は三次元変形関数を持てます。
clipPath,
mask,
pattern
要素は、子孫要素を平坦化して描画した後で適用する必要があり、そのためtransform-style:
preserve-3dの挙動を上書きします。
vector-effectプロパティがnon-scaling-strokeに設定され、かつオブジェクトが3Dレンダリングコンテキスト内にある場合、ストロークには影響しません。
SVGにおける3D変形関数の構文を正式に記述すること(2D関数の仕様のように)。
12. 変形関数
transformプロパティの値は、<transform-function>のリストです。許可される変形関数のセットは以下です。本仕様で<angle>が使われている場合、0に等しい<number>も許可され、0度の角度と同じように扱われます。水平方向の移動のパーセンテージはreference boxの幅に、垂直方向はreference boxの高さに対して相対です。 scale関数のパーセンテージは数値と等価で、指定値では数値としてシリアライズされます。 例:scale3d(50%, 100%, 150%)はscale3d(0.5, 1, 1.5)としてシリアライズされます。
12.1. 2D変形関数
[css-transforms-1]で定義されたscale関数は、パーセンテージも対応するようになりました。
- scale() = scale( [ <number> |
<percentage> ]#{1,2} )
- scaleX() = scaleX( [ <number> | <percentage> ] )
- scaleY() = scaleY( [ <number> | <percentage> ] )
- scaleX() = scaleX( [ <number> | <percentage> ] )
-
css-transforms-1で定義された通りですが、上記の説明のようにパーセンテージも受け付けます。
12.2. 3D変形関数
以下の3d変形関数において、<zero>は0degと同じように扱われます(単位なし0角度はレガシー互換性のため保持)。
- matrix3d() = matrix3d( <number>#{16} )
-
3D変形を16個の値(列優先)の4x4同次行列として指定します。
- translate3d() = translate3d( <length-percentage> , <length-percentage> , <length> )
-
ベクトル[tx,ty,tz]による3D移動を指定します。tx, ty, tzは各パラメータ値です。
- translateZ() = translateZ( <length> )
-
ベクトル[0,0,tz]による3D移動(Z方向のみ)を指定します。
- scale3d() = scale3d( [ <number> | <percentage> ]#{3} )
-
パラメータで示される[sx,sy,sz]ベクトルによる3Dスケール操作を指定します。
- scaleZ() = scaleZ( [ <number> | <percentage> ] )
-
[1,1,sz]ベクトルによる3Dスケール操作(Z方向のみ)を指定します。
- rotate3d() = rotate3d( <number> , <number> , <number> , [ <angle> | <zero> ] )
-
最終パラメータの角度で、最初の3つのパラメータが示す[x, y, z]方向ベクトル周りに3D回転を指定します。正規化できないベクトル(例:[0,0,0])の場合は回転は適用されません。
注: 回転はベクトルの端から原点方向を見るとき、時計回りです。
- rotateX() = rotateX( [ <angle> | <zero> ] )
-
rotate3d(1, 0, 0, <angle>)と同じです。
- rotateY() = rotateY( [ <angle> | <zero> ] )
-
rotate3d(0, 1, 0, <angle>)と同じです。
- rotateZ() = rotateZ( [ <angle> | <zero> ] )
-
rotate3d(0, 0, 1, <angle>)と同じで、2D変形rotate(<angle>)と等価な3D変形です。
- perspective() = perspective( <length [0,∞]> | none )
-
パースペクティブ投影行列を指定します。この行列はZ値に基づいてX・Y座標をスケールし、Zが正なら原点から離れる方向に、Zが負なら原点へ近づく方向に拡大されます。z=0平面上の点は変化しません。パラメータはz=0平面と視点の距離です。値が小さいほどピラミッドが平坦化し、遠近感が強くなります。例:1000pxは中程度の短縮、200pxは極端な遠近感。
深度値が1px未満の場合、レンダリング・解決値計算・補間の終点で、1pxとして扱われます。
注: 上記の1px未満値に関するルールは、perspective()関数を行列に変換する場合を想定しています。
12.3. 変形関数のプリミティブと派生
一部の変形関数は、より汎用的な変形関数で表現できます。これらの変形関数は派生変形関数と呼び、汎用的な変形関数はプリミティブ変形関数と呼びます。三次元プリミティブとその派生変形関数は以下の通りです:
- translate3d()
- <translateX()>、<translateY()>、translateZ()、<translate()>のためのものです。
- scale3d()
- <scaleX()>、<scaleY()>、scaleZ()、<scale()>のためのものです。
- rotate3d()
- <rotate()>、rotateX()、rotateY()、rotateZ()のためのものです。
二次元プリミティブと三次元プリミティブの両方を持つ派生変形関数の場合、使用されるプリミティブは文脈によって決まります。詳細はプリミティブと派生変形関数の補間を参照してください。
13. 行列の補間
2つの行列を補間する場合、各行列は対応する移動量、回転、拡大率、歪み(skew)、(3D行列の場合は)パースペクティブに分解されます。分解された各行列の対応する成分を数値的に補間し、最終ステップで再度行列に合成します。
13.1. 3D行列の補間
13.1.1. 3D行列の分解
以下の疑似コードは「Graphics Gems II(Jim Arvo編集)」の"unmatrix"手法を基にしていますが、オイラー角の代わりにクォータニオンを用いることでギンバルロック問題を回避しています。
次の疑似コードは4x4同次行列に対して動作します:
Input: matrix ; a 4x4 matrix
Output: translation ; a 3 component vector
scale ; a 3 component vector
skew ; skew factors XY,XZ,YZ represented as a 3 component vector
perspective ; a 4 component vector
quaternion ; a 4 component vector
Returns false if the matrix cannot be decomposed, true if it can
// Normalize the matrix.
if (matrix[3][3] == 0)
return false
for (i = 0; i < 4; i++)
for (j = 0; j < 4; j++)
matrix[i][j] /= matrix[3][3]
// perspectiveMatrix is used to solve for perspective, but it also provides
// an easy way to test for singularity of the upper 3x3 component.
perspectiveMatrix = matrix
for (i = 0; i < 3; i++)
perspectiveMatrix[i][3] = 0
perspectiveMatrix[3][3] = 1
if (determinant(perspectiveMatrix) == 0)
return false
// First, isolate perspective.
if (matrix[0][3] != 0 || matrix[1][3] != 0 || matrix[2][3] != 0)
// rightHandSide is the right hand side of the equation.
rightHandSide[0] = matrix[0][3]
rightHandSide[1] = matrix[1][3]
rightHandSide[2] = matrix[2][3]
rightHandSide[3] = matrix[3][3]
// Solve the equation by inverting perspectiveMatrix and multiplying
// rightHandSide by the inverse.
inversePerspectiveMatrix = inverse(perspectiveMatrix)
transposedInversePerspectiveMatrix = transposeMatrix4(inversePerspectiveMatrix)
perspective = multVecMatrix(rightHandSide, transposedInversePerspectiveMatrix)
else
// No perspective.
perspective[0] = perspective[1] = perspective[2] = 0
perspective[3] = 1
// Next take care of translation
for (i = 0; i < 3; i++)
translate[i] = matrix[3][i]
// Now get scale and shear. 'row' is a 3 element array of 3 component vectors
for (i = 0; i < 3; i++)
row[i][0] = matrix[i][0]
row[i][1] = matrix[i][1]
row[i][2] = matrix[i][2]
// Compute X scale factor and normalize first row.
scale[0] = length(row[0])
row[0] = normalize(row[0])
// Compute XY shear factor and make 2nd row orthogonal to 1st.
skew[0] = dot(row[0], row[1])
row[1] = combine(row[1], row[0], 1.0, -skew[0])
// Now, compute Y scale and normalize 2nd row.
scale[1] = length(row[1])
row[1] = normalize(row[1])
skew[0] /= scale[1];
// Compute XZ and YZ shears, orthogonalize 3rd row
skew[1] = dot(row[0], row[2])
row[2] = combine(row[2], row[0], 1.0, -skew[1])
skew[2] = dot(row[1], row[2])
row[2] = combine(row[2], row[1], 1.0, -skew[2])
// Next, get Z scale and normalize 3rd row.
scale[2] = length(row[2])
row[2] = normalize(row[2])
skew[1] /= scale[2]
skew[2] /= scale[2]
// At this point, the matrix (in rows) is orthonormal.
// Check for a coordinate system flip. If the determinant
// is -1, then negate the matrix and the scaling factors.
pdum3 = cross(row[1], row[2])
if (dot(row[0], pdum3) < 0)
for (i = 0; i < 3; i++)
scale[i] *= -1;
row[i][0] *= -1
row[i][1] *= -1
row[i][2] *= -1
// Now, get the rotations out
quaternion[0] = 0.5 * sqrt(max(1 + row[0][0] - row[1][1] - row[2][2], 0))
quaternion[1] = 0.5 * sqrt(max(1 - row[0][0] + row[1][1] - row[2][2], 0))
quaternion[2] = 0.5 * sqrt(max(1 - row[0][0] - row[1][1] + row[2][2], 0))
quaternion[3] = 0.5 * sqrt(max(1 + row[0][0] + row[1][1] + row[2][2], 0))
if (row[2][1] > row[1][2])
quaternion[0] = -quaternion[0]
if (row[0][2] > row[2][0])
quaternion[1] = -quaternion[1]
if (row[1][0] > row[0][1])
quaternion[2] = -quaternion[2]
return true
13.1.2. 分解した3D行列値の補間
分解したtranslation、scale、skew、perspectiveの各成分は、元の行列と移動先行列の対応する成分同士で線形補間されます。
注:
例えば、ソース行列のtranslate[0]と、デスティネーション行列のtranslate[0]は数値的に補間され、その結果がアニメーションする要素の移動量に設定されます。
分解したソース行列のクォータニオンは、分解したデスティネーション行列のクォータニオンと球面線形補間(Slerp)で補間されます。詳細は下記の疑似コード:
Input: quaternionA ; a 4 component vector
quaternionB ; a 4 component vector
t ; interpolation parameter with 0 <= t <= 1
Output: quaternionDst ; a 4 component vector
product = dot(quaternionA, quaternionB)
// Clamp product to -1.0 <= product <= 1.0
product = min(product, 1.0)
product = max(product, -1.0)
if (abs(product) == 1.0)
quaternionDst = quaternionA
return
theta = acos(product)
w = sin(t * theta) / sqrt(1 - product * product)
for (i = 0; i < 4; i++)
quaternionA[i] *= cos(t * theta) - product * w
quaternionB[i] *= w
quaternionDst[i] = quaternionA[i] + quaternionB[i]
return
13.1.3. 3D行列への再合成
補間後、得られた値はユーザースペースで要素を変形するために使用されます。これらの値を使って4x4行列に再合成する方法の一例を下記の疑似コードに示します:
Input: translation ; a 3 component vector
scale ; a 3 component vector
skew ; skew factors XY,XZ,YZ represented as a 3 component vector
perspective ; a 4 component vector
quaternion ; a 4 component vector
Output: matrix ; a 4x4 matrix
Supporting functions (matrix is a 4x4 matrix):
matrix multiply(matrix a, matrix b) returns the 4x4 matrix product of a * b
// apply perspective
for (i = 0; i < 4; i++)
matrix[i][3] = perspective[i]
// apply translation
for (i = 0; i < 4; i++)
for (j = 0; j < 3; j++)
matrix[3][i] += translation[j] * matrix[j][i]
// apply rotation
x = quaternion[0]
y = quaternion[1]
z = quaternion[2]
w = quaternion[3]
// Construct a composite rotation matrix from the quaternion values
// rotationMatrix is a identity 4x4 matrix initially
rotationMatrix[0][0] = 1 - 2 * (y * y + z * z)
rotationMatrix[0][1] = 2 * (x * y - z * w)
rotationMatrix[0][2] = 2 * (x * z + y * w)
rotationMatrix[1][0] = 2 * (x * y + z * w)
rotationMatrix[1][1] = 1 - 2 * (x * x + z * z)
rotationMatrix[1][2] = 2 * (y * z - x * w)
rotationMatrix[2][0] = 2 * (x * z - y * w)
rotationMatrix[2][1] = 2 * (y * z + x * w)
rotationMatrix[2][2] = 1 - 2 * (x * x + y * y)
matrix = multiply(matrix, rotationMatrix)
// apply skew
// temp is a identity 4x4 matrix initially
if (skew[2])
temp[2][1] = skew[2]
matrix = multiply(matrix, temp)
if (skew[1])
temp[2][1] = 0
temp[2][0] = skew[1]
matrix = multiply(matrix, temp)
if (skew[0])
temp[2][0] = 0
temp[1][0] = skew[0]
matrix = multiply(matrix, temp)
// apply scale
for (i = 0; i < 3; i++)
for (j = 0; j < 4; j++)
matrix[i][j] *= scale[i]
return
14. プリミティブおよび派生変形関数の補間
同じ名前かつ同じ引数数を持つ2つの変形関数は、変換なしに数値的に補間されます。計算された値は、同じ変形関数型・同じ引数数になります。<matrix()>、<matrix3d()>、<perspective()>には特別なルールが適用されます。
<matrix()>、matrix3d()、perspective()の変形関数は、まず4x4行列に変換され、その後行列の補間の節で定義された方法で補間されます。
プリミティブrotate3d()で補間する場合、変形関数の方向ベクトルをまず正規化します。正規化ベクトルが一致せず、かつ両方の回転角が非ゼロの場合、変形関数はまず4x4行列に変換され、その後行列の補間の節で定義された方法で補間されます。そうでなければ、回転角だけ数値的に補間され、非ゼロ角の回転ベクトル、または両方ゼロの場合は(0, 0, 1)が使われます。
translate(0)とtranslate(100px)は同じ型・同じ引数数なので数値的に補間できます。translateX(100px)は型が異なり、translate(100px, 0)は引数数が異なるので、これらの変形関数は変換なしでは補間できません。
同じプリミティブを共有する型違いの変形関数、または同じ型で引数数が異なる変形関数も補間可能です。両方の変形関数はまず共通のプリミティブに変換され、その後数値的に補間されます。算出値はプリミティブ型+補間された引数となります。
次の例は、divボックスにマウスオーバーした際にtranslateX(100px)からtranslateY(100px)へ3秒で遷移する様子を示します。両方の変形関数は同じプリミティブtranslate()由来なので補間可能です。
div {
transform : translateX ( 100 px );
}
div:hover {
transform : translateY ( 100 px );
transition : transform 3 s ;
}
遷移中は両方の変形関数が共通のプリミティブに変換されます。translateX(100px)はtranslate(100px, 0)に、translateY(100px)はtranslate(0, 100px)に変換され、以降数値的に補間できます。
両方の変形関数が二次元空間のプリミティブを共有する場合は、両方とも二次元プリミティブに変換されます。一方または両方が三次元変形関数なら、共通の三次元プリミティブが使われます。
この例では、二次元変形関数が三次元変形関数へアニメーションされます。共通プリミティブはtranslate3d()です。
div {
transform : translateX ( 100 px );
}
div:hover {
transform : translateZ ( 100 px );
transition : transform 3 s ;
}
まずtranslateX(100px)はtranslate3d(100px, 0, 0)に、translateZ(100px)はtranslate3d(0, 0, 100px)に変換されます。その後、両方の変形関数が数値的に補間されます。
15. 変形リストの加算と累積
Vresult = Va + Vb - 1
div. animate( { transform: [ 'scale(1)' , 'scale(2)' ] }, { duration: 1000 , easing: 'ease' , } );
次のように拡張した場合も期待通りに動作します:
div. animate( { transform: [ 'scale(1)' , 'scale(2)' ] }, { duration: 1000 , easing: 'ease' , iterations: 5 , iterationComposite: 'accumulate' , } );
15.1. 加算のニュートラル要素
一部のアニメーションでは加算のニュートラル要素が必要です。変形関数の場合、これは0のスカラーまたは0スカラーのリストです。例としてはtranslate(0)、translate3d(0, 0, 0)、translateX(0)、translateY(0)、translateZ(0)、scale(0)、scaleX(0)、scaleY(0)、scaleZ(0)、rotate(0)、rotate3d(vx, vy, vz, 0)(vは文脈依存ベクトル)、rotateX(0)、rotateY(0)、rotateZ(0)、skew(0, 0)、skewX(0)、skewY(0)、matrix(0, 0, 0, 0, 0, 0)、matrix3d(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)、perspective(none)などが挙げられます。
注: 加算のニュートラル要素へのアニメーションや、そこからのアニメーションでは、<matrix()>、matrix3d()、perspective()は離散アニメーションにフォールバックします(§ 13 行列の補間参照)。
16. 変形関数の数学的記述
数学的には、すべての変形関数は次の形の4x4変換行列として表現できます:
$$\begin{bmatrix} m11 & m21 & m31 & m41 \\ m12 & m22 & m32 & m42 \\ m13 & m23 & m33 & m43 \\ m14 & m24 & m34 & m44 \end{bmatrix}$$
行列上の1単位の移動は、要素のローカル座標系における1ピクセルに相当します。
-
パラメータtx、ty、tzによる3D移動は、次の行列と等価です:
$$\begin{bmatrix} 1 & 0 & 0 & tx \\ 0 & 1 & 0 & ty \\ 0 & 0 & 1 & tz \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
-
パラメータsx、sy、szによる3Dスケールは、次の行列と等価です:
$$\begin{bmatrix} sx & 0 & 0 & 0 \\ 0 & sy & 0 & 0 \\ 0 & 0 & sz & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
-
ベクトル[x,y,z]とパラメータalphaによる3D回転は、次の行列と等価です:
$$\begin{bmatrix} 1 - 2 \cdot (y^2 + z^2) \cdot sq & 2 \cdot (x \cdot y \cdot sq - z \cdot sc) & 2 \cdot (x \cdot z \cdot sq + y \cdot sc) & 0 \\ 2 \cdot (x \cdot y \cdot sq + z \cdot sc) & 1 - 2 \cdot (x^2 + z^2) \cdot sq & 2 \cdot (y \cdot z \cdot sq - x \cdot sc) & 0 \\ 2 \cdot (x \cdot z \cdot sq - y \cdot sc) & 2 \cdot (y \cdot z \cdot sq + x \cdot sc) & 1 - 2 \cdot (x^2 + y^2) \cdot sq & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
ここで:
$$sc = \sin (\alpha/2) \cdot \cos (\alpha/2)$$ $$sq = \sin^2 (\alpha/2)$$
そしてx, y, zは正規化済み(すなわち、与えられたx, y, z値を2乗和の平方根で割ったもの)です。
これにより、X軸回転は次のように単純化されます:$$\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 - 2 \cdot sq & -2 \cdot sc & 0 \\ 0 & 2 \cdot sc & 1 - 2 \cdot sq & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
Y軸回転は次のように単純化されます:
$$\begin{bmatrix} 1 - 2 \cdot sq & 0 & 2 \cdot sc & 0 \\ 0 & 1 & 0 & 0 \\ -2 \cdot sc & 0 & 1 - 2 \cdot sq & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
Z軸回転は次のように単純化されます:
$$\begin{bmatrix} 1 - 2 \cdot sq & -2 \cdot sc & 0 & 0 \\ 2 \cdot sc & 1 - 2 \cdot sq & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
-
パラメータdによるパースペクティブ投影行列は、次の行列と等価です:
$$\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & -1/d & 1 \end{bmatrix}$$
パラメータdがnoneの場合は無限大とみなし(結果の行列は恒等行列になります)。
17. SVGの transform 属性
本仕様では、新たな提示属性として transform-origin、perspective、perspective-origin、transform-style、backface-visibilityも導入されます。
新しく導入された提示属性の値は、SVGデータ型 [SVG11] の構文規則に従ってパースされます。
18. SVGアニメーション
18.1.
animate
要素および
set
要素
導入された提示属性 perspective、perspective-origin、transform-style、backface-visibilityはアニメーション可能です。transform-styleとbackface-visibilityは非加算型です。
19. その他の課題
https://lists.w3.org/Archives/Public/www-style/2015Mar/0371.html の通り、WGは変形を統一的な「scale」に分解する式を追加することを決定しました (仕様ではscaleX/Y/Zへの分解方法は既に定義済み)。 これはSVGのnon-scaling stroke仕様などで利用されます。式の定義はこちら。
20. セキュリティおよびプライバシーに関する考慮事項
この仕様では新たなセキュリティやプライバシーの考慮事項は導入されません。
変更履歴
最近の変更
2020年3月3日WDからの重要な変更点:
-
この仕様は個別変形プロパティが2Dか3Dかの状態管理を要求しなくなり、2Dで表現可能な値は2Dとして扱うことを要求します(#3305参照)。
注: 類似の変更は変形関数にも意図されていますが、まだ反映されていません。
- scale プロパティおよび scale()、scaleX()、scaleY() 関数がパーセンテージ対応になりました(#3399参照)。
-
仕様の複数箇所の定義を3Dレンダリングコンテキストの定義と整合するよう修正しました:
- 3Dレンダリングコンテキストを確立する要素のborder、背景、装飾は、3Dシーン内のz=0で描画される(背後ではなく)(#6238参照)。
- 累積3D変換行列に、確立要素のtransformや親のperspectiveを含める(#6191参照)。
- ペイント包含はグループ化プロパティであることを定義(#6202参照)。
- none引数がperspective()でサポート(#6488参照)。
- perspective()の値のクランプは解決値や補間にも適用される(#6320および#6346参照)。
- preserve-3dの効果は変形可能要素にのみ影響することを明確化(#6430参照)。
- 加算のニュートラル要素としてperspective()はperspective(none)であることを修正
- translateの解決値にパーセンテージが含まれる旨を注記追加(#2124参照)。
- 3Dソートの説明をより正確にし、どの子孫が含まれるか明示し、Appendix Eの参照を手順1〜7に限定しないよう修正(#926参照)。