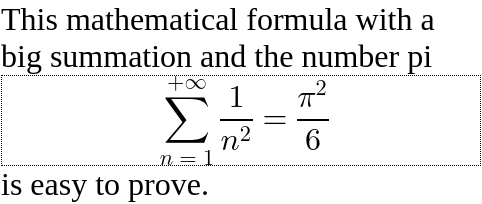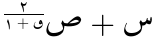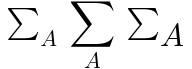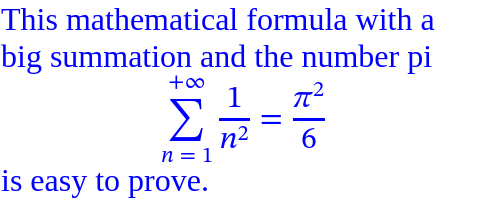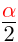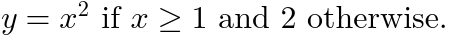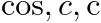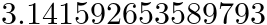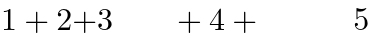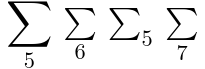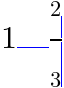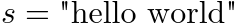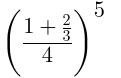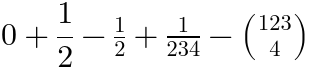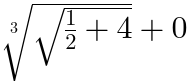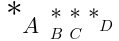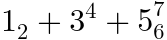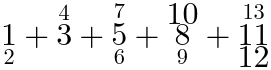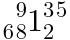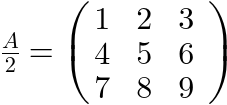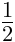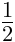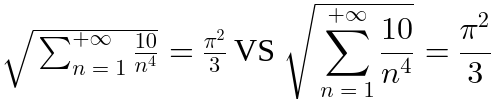概要
この仕様は、ブラウザー実装に適した数式マークアップ言語(MathML)のコアサブセットを定義します。
MathMLは数式表記を記述し、その構造と内容の両方を保持するためのマークアップ言語です。
MathMLの目標は、HTMLがテキストに対して可能にしたように、数学をワールドワイドウェブで配信・受信・処理できるようにすることです。
目次
概要 この文書のステータス 1. 導入2. MathMLの基礎
2.1
要素と属性
2.1.1 最上位 <math> 要素2.1.2 MathML属性値の型2.1.3
グローバル属性2.1.4
HTML要素とMathML要素に共通の属性2.1.5 レガシーMathMLスタイル属性2.1.6
displaystyle属性とscriptlevel属性2.1.7 有効として予約された属性
2.2 ウェブプラットフォームへの統合
2.2.1
HTMLとSVG2.2.2
CSSスタイリング2.2.3
DOMとJavaScript2.2.4
テキストレイアウト2.2.5
フォーカス
3. 表示マークアップ
3.1
視覚的フォーマットモデル
3.1.1
ボックスモデル3.1.2
レイアウトアルゴリズム3.1.3
匿名の <mrow> ボックス3.1.4
スタッキングコンテキスト
3.2
トークン要素
3.2.1
テキスト<mtext>
3.2.1.1 <mtext>のレイアウト
3.2.2
識別子<mi>3.2.3
数値<mn>3.2.4 演算子、フェンス、セパレータ、アクセント
<mo>
3.2.4.1 装飾付き演算子3.2.4.2 辞書ベース属性3.2.4.3 演算子のレイアウト
3.2.5
スペース<mspace>
3.2.5.1
スペース類似要素の定義
3.2.6
文字列リテラル<ms>
3.3
一般的レイアウトスキーマ
3.3.1 部分式のグループ化<mrow>
3.3.1.1 ブロック軸方向の演算子伸長アルゴリズム3.3.1.2 <mrow>のレイアウト
3.3.2
分数<mfrac>
3.3.2.1
分数線が非ゼロの場合3.3.2.2
分数線がゼロの場合
3.3.3
根号<msqrt>, <mroot>
3.3.3.1 根号記号3.3.3.2 平方根3.3.3.3 添字付き根号
3.3.4
スタイル変更<mstyle>3.3.5
エラーメッセージ<merror>3.3.6 内容周囲スペース調整
<mpadded>
3.3.6.1
内側ボックスと要求パラメータ3.3.6.2 <mpadded>のレイアウト
3.3.7
部分式の不可視化<mphantom>
3.4
添字とリミットの構成要素
3.4.1
下付き・上付き<msub>,
<msup>, <msubsup>
3.4.1.1 <msub>,
<msup>, <msubsup>の子3.4.1.2 下付き付き基底3.4.1.3 上付き付き基底3.4.1.4
下付き・上付き付き基底
3.4.2 下付き・上付き
<munder>, <mover>,
<munderover>
3.4.2.1
子要素: <munder>,
<mover>, <munderover>3.4.2.2 インライン軸に沿った演算子の伸長アルゴリズム3.4.2.3 下付き付き基底3.4.2.4 上付き付き基底3.4.2.5
下付きおよび上付き付き基底
3.4.3
プレスクリプトおよびテンソル指数<mmultiscripts>
3.4.3.1
基底とプレ/ポストスクリプト
3.4.4 Displaystyle, scriptlevel, math-shift のスクリプト内での挙動
3.5 表形式の数学
3.5.1 表または行列<mtable>3.5.2 表または行列の行<mtr>3.5.3 表または行列のセル<mtd>
3.6
式への動きの付与3.7
意味情報とプレゼンテーション
4.
数式レイアウト用CSS拡張
4.1
display: block math
およびdisplay: inline math値4.2
math-auto変換4.3
math-styleプロパティ4.4
math-shiftプロパティ4.5
math-depthプロパティ
5. OpenType
MATHテーブル
5.1
レイアウト定数(MathConstants)5.2 グリフ情報(MathGlyphInfo)5.3 演算子のサイズバリエーション(MathVariants)
5.3.1 GlyphAssemblyテーブル5.3.2 グリフ伸長アルゴリズム
A.
ユーザーエージェントスタイルシート B. 演算子テーブル
B.1
演算子辞書B.2
演算子辞書(人間可読)B.3 結合文字の同等性B.4
Unicodeベースのグリフアセンブリ
C.
数学的英数字記号
C.1
italicマッピング
D.
謝辞E.
セキュリティの考慮事項F.
プライバシーの考慮事項G. 適合性H. 参考文献
H.1
規範的参考文献H.2
参考情報的参考文献
用語 MathML 要素 は
MathML 名前空間 の任意の要素を指します。
この仕様で定義される MathML 要素は
MathML コア要素 と呼ばれており、以下に一覧があります。
下記以外の MathML 要素は
未知の MathML 要素 と呼びます。
annotation annotation-xml maction math merror mfrac mi mmultiscripts mn mo mover mpadded mphantom mprescripts mroot mrow ms mspace msqrt mstyle msub msubsup msup mtable mtd mtext mtr munder munderover semantics
グループ化要素 は
maction math merror mphantom mprescripts mrow mstyle semantics 未知の MathML 要素 です。
スクリプト要素 は
mmultiscripts mover msub msubsup msup munder munderover
根号要素 は
mroot msqrt
この仕様で定義される属性には名前空間がなく、
MathML属性
と呼ばれます:
MathML は、文書内の各 MathML マークアップのインスタンスをカプセル化する単一の最上位(ルート) math 要素を指定します。他のすべての
MathML コンテンツは <math> 要素内になければなりません。
<math> 要素は 2.1.3
グローバル属性
display
属性がある場合、
ASCII 大文字・小文字を区別せず
block または inline と一致する必要があります。
A.
ユーザーエージェントスタイルシート block math または inline math)
および math-stylenormal または compact)プロパティが記述されています。
属性が無い場合や無効な値の場合、ユーザーエージェントスタイルシートはそれを inline と同じように扱います。
この仕様は alttext 属性に固有の可観測な動作を定義しません。
Note
alttext
属性は数式レイアウトを実装していない一部のレガシーシステムで代替テキストとして用いられる場合があります。
<math> 要素で計算される
display block math や inline math でない場合は、CSS
仕様で記述された該当の値によりレイアウトされます。そうでない場合は
mrow math content box
を生成します。その math content box
が、要素のレイアウト内容として利用されます(CSS の display: block や display: inline の場合)。
さらに、計算結果が block math の場合は、その math content box は
コンテナ内で水平中央にレンダリングされます。
Note
TE X の display mode $$...$$ と inline mode $...$ は、
それぞれ display="block" および display="inline" に対応します。
次の例では、math
<div style ="width: 15em;" >
This mathematical formula with a big summation and the number pi
<math display ="block" style ="border: 1px dotted black;" >
<mrow >
<munderover >
<mo > ∑</mo >
<mrow > <mi > n</mi > <mo > =</mo > <mn > 1</mn > </mrow >
<mrow > <mo > +</mo > <mn > ∞</mn > </mrow >
</munderover >
<mfrac >
<mn > 1</mn >
<msup > <mi > n</mi > <mn > 2</mn > </msup >
</mfrac >
</mrow >
<mo > =</mo >
<mfrac >
<msup > <mi > π</mi > <mn > 2</mn > </msup >
<mn > 6</mn >
</mfrac >
</math >
is easy to prove.
</div > 比較として、同じ数式をインラインモードで表示した場合、強制改行なしでテキスト段落内に埋め込まれます。
mrow
適切な数学レンダリングには数学フォントの利用が必要なため、
ユーザーエージェントスタイルシート
では <math> 要素で font-family を
親要素から継承せず math
に設定すべきです。また親コンテナで設定されることのある font-style、font-weight、
direction、text-indent などの CSS
プロパティは数式自体には適用されないため、ユーザーエージェントスタイルシートでそれらをデフォルトでリセットする規則があります。
math {
direction : ltr;
text-indent : 0 ;
letter-spacing : normal;
line-height : normal;
word-spacing : normal;
font-family : math;
font-size : inherit;
font-style : normal;
font-weight : normal;
display : inline math;
math-shift : normal;
math-style : compact;
math-depth : 0 ;
}
math[display="block" i] {
display : block math;
math-style : normal;
}
math[display="inline" i] {
display : inline math;
math-style : compact;
}
CSSデータ型に加え、いくつかのMathML属性は次のMathML固有型に依存します。
unsigned-integer
[CSS-VALUES-4 <integer> 値で、最初の文字が
U+002D ハイフン記号(-)でも
U+002B プラス記号(+)でもないもの。
boolean
ASCII大文字小文字区別なし で
true か false に一致する文字列。
以下の属性はすべてのMathML要素に共通で指定できます。
id 、
class 、
style 、
data-*autofocus 、および
nonce 、
tabindex
属性は、HTML要素で定義されているものと同じ構文と意味です。
dir 属性が存在する場合、
ASCII大文字小文字区別なし で ltr または rtl と一致していなければなりません。
その場合、ユーザーエージェントはその属性を
呈示用ヒント として要素の
direction
プロパティに対応付けて扱うこととなります。
具体的には、rtl との一致は rtl に、
ltr との一致は ltr にマップされます。
次の例では、dir
属性を使い「𞸎 + 𞸑 のべき(٢ 分の 𞸟 + ١)」を
右から左にレンダリングしています。
<math dir ="rtl" >
<mrow >
<mi > 𞸎</mi >
<mo > +</mo >
<msup >
<mi > 𞸑</mi >
<mfrac >
<mn > ٢</mn >
<mrow >
<mi > 𞸟</mi >
<mo > +</mo >
<mn > ١</mn >
</mrow >
</mfrac >
</msup >
</mrow >
</math >
すべてのMathML要素は、HTMLのイベントハンドラー属性 同様にイベントハンドラー属性をサポートします。
すべてのイベントハンドラー属性は
HTMLで
HTMLElements がサポートするもの と同様に、MathML要素でも MathMLElement IDL
によりサポートされます。
mathcolor 、
mathbackground
属性がある場合、値は
<color> 型でなければなりません。
この場合、ユーザーエージェントは属性を
呈示用ヒント として、要素の
color および
background-color
プロパティに対応する値として設定します。
mathcolor属性はMathMLのテキストやバーなどの前景色を、
mathbackground属性は要素の背景色を示します。
mathsize
属性がある場合、有効な
<length-percentage>
でなければなりません。
この場合、ユーザーエージェントは属性を
呈示用ヒント として
要素のfont-size プロパティに設定します。
mathsizeプロパティは数式中のグリフの高さを示し、それに応じて他の要素(スペーシングやシフト、バーの線の太さなど)も拡縮されます。
Note
これらの属性はフルMathMLとの互換のために実装されています。MathML Coreのみを対象にする場合はCSSスタイリングを使用することが推奨されます。
displaystyle
属性がある場合、値はboolean 型でなければなりません。
この場合、ユーザーエージェントは属性を
呈示用ヒント として要素の
math-styleASCII大文字小文字区別なし でtrueはnormalに、falseはcompactにマップされます。
この属性は、数式の論理的高さ(値がfalseの場合に内容サイズやスクリプト配置を変更することで高さを最小化)を最小化するか否かを示します。
scriptlevel
属性がある場合、値は
+<U>、-<U>、<U>
のいずれかで、<U>は
unsigned-integer 型です。
この場合、ユーザーエージェントは
scriptlevel属性を
呈示用ヒント として要素の
math-depth+<U>、-<U>、<U> はそれぞれ
add(<U>)、
add(<-U>)、
<U> にマップされます。
displaystylescriptlevelA.
ユーザーエージェントスタイルシート font-size: math がデフォルト指定され、scriptlevel の変化が反映されます。
この例では、munder displaystyle がtrueだとΣが大きく描画され「A」は下付きとなり、scriptlevel を「A」に0指定すると最上位math要素と同じフォントサイズになります。
<math >
<munder >
<mo > ∑</mo >
<mi > A</mi >
</munder >
<munder displaystyle ="true" >
<mo > ∑</mo >
<mi > A</mi >
</munder >
<munder >
<mo > ∑</mo >
<mi scriptlevel ="0" > A</mi >
</munder >
</math >
Note
T
E X の
\displaystyle、
\textstyle、
\scriptstyle、
\scriptscriptstyleはそれぞれ
displaystyle(true/false)・
scriptlevel(0/1/2)の組み合わせに対応します。
intent 、
arg
属性は有効として予約されています。
この仕様ではintentarg
Note
これら属性は[
MATHML4 ]で説明されており、
今後のバージョンで定義されるかどうかは未定です。現在開発中で今後変更される可能性がありますので、著者は注意してください。
表示マークアップにおけるトークン要素は、意味を持つ数学記法の最小単位を表現することを広く意図しています。トークンは大まかに言えば、テキスト中の単語に相当します。しかし、数学記法の厳密かつ記号的な性質のため、さまざまなカテゴリやトークン要素のプロパティが
MathML マークアップにおいて重要な役割を果たします。対照的に、テキストデータでは、個々の単語が特別にマークアップされたりスタイル付けされる必要はほとんどありません。
注
実際には、ほとんどの MathML トークン要素は変数や数値、演算子などの単純なテキストのみを含み、高度なレイアウトは必要としません。しかし、改行を含むテキストや、任意の HTML5
フレージング要素を含めることもできます。
mtext
要素は、そのままレンダリングすべき任意のテキストを表現するために使用します。一般的に、<mtext> 要素は注釈テキストを示すことを意図しています。
<mtext> 要素は 2.1.3
グローバル属性
次の例では、
mtext
<math >
<mi > y</mi >
<mo > =</mo >
<mrow >
<msup >
<mi > x</mi >
<mn > 2</mn >
</msup >
<mtext > if </mtext >
<mrow >
<mi > x</mi >
<mo > ≥</mo >
<mn > 1</mn >
</mrow >
<mtext > and </mtext >
<mn > 2</mn >
<mtext > otherwise.</mtext >
</mrow >
</math >
この要素の算出
display block math または inline math でない場合、対応する値が記述されている CSS
仕様に従ってレイアウトされます。それ以外の場合は、以下のレイアウトが行われます。
<mtext> 要素が
強制改行 や ソフトラップの機会 を含まないテキストコンテンツのみから成る場合は、そのテキストのために生成される匿名子ノードが該当する CSS
仕様で定められた通りにレイアウトされ、かつ次の通りです:
それ以外の場合、mtext 要素は ブロックボックス としてレイアウトされ、対応する min-content inline
size 、max-content inline size 、inline size 、block size 、first
baseline set および last baseline set が math content
box のために用いられます。
mi
要素は、記号名や
任意のテキスト
を識別子としてレンダリングするために使用します。識別子には変数、関数名、記号定数などが含まれます。
<mi> 要素は 2.1.3
グローバル属性
レイアウトアルゴリズムは
mtext ユーザーエージェントスタイルシート
には、自動イタリックを 4.2
math-auto 変換
mi {
text-transform : math-auto;
}
mathvariant
属性が存在する場合は
ASCII大文字・小文字を区別しない
形で normal と一致しなければなりません。
その場合、ユーザーエージェントはこの属性をプレゼンテーションヒントとみなし、
要素の
text-transform
プロパティを none に設定します。それ以外の場合、この属性は効果を持ちません。
注
[MathML3 mathvariant
属性はトークン要素の論理クラスを定義するために使用され、それぞれのクラスは特定の意味を持つ書体的に関連した記号トークンの集合を提供していました。
MathML Core では、この属性は
mi UNICODE C.
数理用英数字記号
次の例では、
mi 4.2
math-auto 変換text-transform: math-auto の効果は、
最初の <mi> にはありません("cos" は3文字で構成されるため)、
2番目の <mi> は数学イタリック体でレンダリングされます("c" は1文字、U+0063 ラテン小文字 c で、
イタリック テーブルに従い U+1D450 数学イタリック小文字 c にマッピングされます)、
3番目の <mi> には効果がありません(mathvariant="normal" により、
text-transform が none になる)、4番目の
<mi> にも効果がありません(U+221E 無限大のイタリックテーブルにマッピングが定義されていない)。
<math >
<mi > cos</mi >
<mo > ,</mo >
<mi > c</mi >
<mo > ,</mo >
<mi mathvariant ="normal" > c</mi >
<mo > ,</mo >
<mi > ∞</mi >
</math >
mn
要素は「数値リテラル」や
数値リテラルとしてレンダリングされるべき他のデータを表します。一般的に、数値リテラルは桁(数字)の並びであり、おそらく小数点を含む、符号なし整数または実数を表します。
<mn> 要素は 2.1.3
グローバル属性mtext
次の例では、
mn
<math >
<mn > 3.141592653589793</mn >
</math >
mo
要素は、演算子または演算子としてレンダリングされるべきもの全般を表します。
一般に、数学演算子の記法上の慣習は非常に複雑であるため、MathMLは<mo>要素のレンダリング動作を指定するために比較的高度な仕組みを提供します。
その結果、MathMLにおいて「演算子としてレンダリングされるべきもの」には、通常意味での数学演算子以外の記号も多く含まれます。中置・前置・後置の通常の演算子のほか、波括弧や括弧、絶対値バーといったフェンス記号、カンマやセミコロン等のセパレータ、シンボル上のバーやチルダなどの数学アクセントも該当します。本章では「演算子」という用語をこの広い意味で用います。
<mo>要素は2.1.3
グローバル属性
本仕様はfence 属性及びseparator 属性に対して特有の可観測な動作は定義しません。
以下の例では、
mo formlspace rspace
<math >
<mn > 1</mn >
<mo > +</mo >
<mn > 2</mn >
<mo form ="prefix" > +</mo >
<mn > 3</mn >
<mo lspace ="2em" > +</mo >
<mn > 4</mn >
<mo rspace ="3em" > +</mo >
<mn > 5</mn >
</math >
他の用途は、和記号のような大きい演算子です。
displaystyle が true の場合、その演算子は大きく描画されますが、
largeop displaystyle が false の場合、下付きが実際には下付き文字として描画されますが、
movablelimits
<math >
<mrow displaystyle ="true" >
<munder >
<mo > ∑</mo >
<mn > 5</mn >
</munder >
<munder >
<mo largeop ="false" > ∑</mo >
<mn > 6</mn >
</munder >
</mrow >
<mrow >
<munder >
<mo > ∑</mo >
<mn > 5</mn >
</munder >
<munder >
<mo movablelimits ="false" > ∑</mo >
<mn > 7</mn >
</munder >
</mrow >
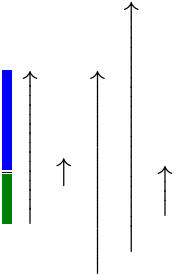
</math > 演算子は、フェンスやアクセント、矢印などの伸縮可能な記号としても使われます。次の例では、縦の矢印が
mspace stretchy symmetric minsize maxsize
<math >
<mfrac >
<mspace height ="50px" depth ="50px" width ="10px" style ="background: blue" />
<mspace height ="25px" depth ="25px" width ="10px" style ="background: green" />
</mfrac >
<mo > ↑</mo >
<mo stretchy ="false" > ↑</mo >
<mo symmetric ="true" > ↑</mo >
<mo minsize ="250px" > ↑</mo >
<mo maxsize ="50px" > ↑</mo >
</math > 演算子のデフォルトプロパティは3.2.4.2
辞書ベース属性
mspace
空要素は、その属性によって設定された任意のサイズの空白を表す。
<mspace> 要素は、
2.1.3 グローバル属性
width ,
height ,
depth
が存在する場合、
その値は有効な <length-percentage>
でなければならない。
width 属性が存在し、有効でありパーセントでない場合、
その属性は要素の 表示ヒント
として、その要素の width
プロパティに対応する値を設定するために使われる。
height 属性が存在せず、有効でないかパーセントの場合、要求された line-ascent は 0 となる。
それ以外の場合は height 属性の解決値で負の値は 0 に丸める。
height 属性と depth 属性の両方が存在し、有効でかつパーセントでない場合、
それらは 表示ヒント
として使われ、要素の height
プロパティに "calc(", height 属性値, " + ", depth
属性値, ")" を連結した値を設定する。
どちらか一方だけが存在し有効かつパーセントでない場合、それは
表示ヒント
としてその要素の height
プロパティに対応する値を設定する。
次の例では
mspace
<math >
<mn > 1</mn >
<mspace width ="1em"
style ="border-top: 1px solid blue" />
<mfrac >
<mrow >
<mn > 2</mn >
<mspace depth ="1em"
style ="border-left: 1px solid blue" />
</mrow >
<mrow >
<mn > 3</mn >
<mspace height ="2em"
style ="border-left: 1px solid blue" />
</mrow >
</mfrac >
</math >
<mspace> 要素の計算された
display block math または inline math と等しくない場合、
対応する値が記述されている CSS 仕様に従ってレイアウトされる。
それ以外の場合、
<mspace> 要素は
図 9 のようにレイアウトされる。
min-content inline size 、
max-content inline size および inline size は
width プロパティの解決値と等しい。
block size は height プロパティの解決値と等しい。
line-ascent は上記で決定された要求された line-ascent と等しい。
図 9
<mspace> 要素のボックスモデル
多くの MathML 表示要素は「スペース類似(space-like)」であり、通常は空白としてレンダリングされ、
それが現れる式の数学的意味には影響しない。
そのため、これらの要素は他の MathML 式の中でもやや例外的な動作をする場合が多い。
MathML コア要素 は
もし次のいずれかであれば、
スペース類似要素
となる:
mtext mspace
あるいは、全ての フロー内 子要素が スペース類似
である グループ化要素
または
mpadded
同じ定義がビジュアルフォーマットモデルのボックスにも適用され、
匿名 <mrow> ボックス は
グループ化要素 として扱われる。
注
mphantom
は、その内容がスペース類似でない限り、自動的にスペース類似とは見なされない点に注意。
これは、隣接する要素がスペース類似かどうかで演算子スペースが影響を受けるためである。
<mphantom> 要素は主として式の整列の補助を意図しており、
<mphantom> の隣の演算子は
<mphantom> の内容があるかのように挙動するべきであり、
等しい大きさの空白領域の隣であるかのように振る舞うべきではない。
ms
要素は、コンピュータ代数システムや「プログラム言語」を含む他のシステムによって解釈されるような式内の
「文字列リテラル」を表す用途で使う。
<ms> 要素は
2.1.3 グローバル属性mtext
次の例では
ms
<math >
<mi > s</mi >
<mo > =</mo >
<ms > "hello world"</ms >
</math >
注
MathML3 では
lquote 属性や
rquote 属性で
それぞれ開き引用符と閉じ引用符として使う文字列を指定できたが、
これらはサポートされなくなり、
引用符は
<ms> 要素内部のテキストとして指定しなければならない。
レガシードキュメントの視覚表現を保持するためには CSS ルールを追加できる。
例えば左から右方向の場合:
ms:before , ms:after {
content : "\0022" ;
}
ms[lquote] :before {
content : attr (lquote);
}
ms[rquote] :after {
content : attr (rquote);
}
トークン以外にも、いくつかの MathML
表示要素のファミリーが存在する。一つのファミリーは添字や上付き文字などの各種「スクリプト」記法を扱う。もう一つのファミリーは行列やテーブルに関係する。本節で述べるその他の要素は、分数や根号などの基本記法や、スタイルプロパティの設定やエラー処理などの汎用的な機能を扱う。
mrow
要素は、一つ以上の部分式をまとめてグループ化するために使う。通常、演算子として働く <mo> 要素一つ以上と、それらの「オペランド」となる式から構成される。
次の例では
mrow mfrac msup mrow mo
mrow アルファベットベースライン または数学ベースライン に従う)が適切に行われ、囲い記号は垂直方向に伸長され、+演算子の前後のスペースも自動的に調整される。
<math >
<msup >
<mrow >
<mo > (</mo >
<mfrac >
<mrow >
<mn > 1</mn >
<mo > +</mo >
<mfrac >
<mn > 2</mn >
<mn > 3</mn >
</mfrac >
</mrow >
<mn > 4</mn >
</mfrac >
<mo > )</mo >
</mrow >
<mn > 5</mn >
</msup >
</math >
<mrow> 要素は
2.1.3 グローバル属性<mrow> 要素の フロー内 子要素 child1 ,
child2 , …, childN
は 図 10 の通りにレイアウトされる。子ボックスは横一列に順次配置され、そのすべての
アルファベットベースライン
が揃えられる。
図 10
<mrow> 要素のボックスモデル
図
11 ブロック軸方向における演算子の対称・非対称伸長
ブロック軸方向の演算子伸長アルゴリズム
は、以下の手順から成る:
ブロック伸長サイズ制約
または インライン伸長サイズ制約
が存在する場合、レイアウトされる要素は
装飾演算子 である。同じサイズ制約で
フロー内 子のうち装飾演算子であるもの1つをレイアウトし、他の フロー内 子は
サイズ制約なしでレイアウトし、終了する。
それ以外の場合、
フロー内 子のリストを
LToStretch (装飾演算子 かつ
stretchystretch axis がある)と
LNotToStretch に分割する。
LNotToStretch のすべてに伸長サイズ制約なしでレイアウトを行う。
LToStretch が空なら終了。
LNotToStretch が空の場合は
LToStretch のすべてに
ブロック伸長サイズ制約
(0, 0) でレイアウトを行う。
前のステップでレイアウトした フロー内 子の マージンボックス のうち
最大のインクアセント・最大のインクディセントを
それぞれ Uascent ,
Udescent として求める。
LToStretch の全要素を
ブロック伸長サイズ制約
(Uascent , Udescent ) で(再)レイアウト。
mfrac
要素は分数に用いられる。二項係数やルジャンドル記号など分数型オブジェクトもマークアップ可能。
<mfrac> 要素の計算された
display block math
または inline math でない場合、該当するCSS仕様に従ってレイアウトされる。
それ以外は以下のレイアウトになる。
<mfrac> 要素は
2.1.3 グローバル属性
linethickness
属性は、分数バーとして用いる 分数線の太さ
を示す。指定がある場合、その値は有効な <length-percentage>
でなければならない。
属性がない場合や無効な値なら
FractionRuleThickness がデフォルト値となる。
パーセント値はデフォルト値に相対的に解釈。
負の値は0と解釈される。
次の例は 4 つの異なる
linethickness displaystyle
でない分数は、隙間やフォントサイズが小さい。
<math >
<mn > 0</mn >
<mo > +</mo >
<mfrac displaystyle ="true" >
<mn > 1</mn >
<mn > 2</mn >
</mfrac >
<mo > −</mo >
<mfrac >
<mn > 1</mn >
<mn > 2</mn >
</mfrac >
<mo > +</mo >
<mfrac linethickness ="200%" >
<mn > 1</mn >
<mn > 234</mn >
</mfrac >
<mo > −</mo >
<mrow >
<mo > (</mo >
<mfrac linethickness ="0" >
<mn > 123</mn >
<mn > 4</mn >
</mfrac >
<mo > )</mo >
</mrow >
</math >
<mfrac> 要素は
displaystylefalse に、
もしくは既に false なら
scriptlevelmath-shift を
compact に設定。
分数線と周辺要素(例えばマイナス記号や他の分数線等)の混同を避けるため、デフォルトで1ピクセルのスペースを要素の周囲に追加する。
ユーザーエージェントスタイルシート
には次のルールが必須:
mfrac {
padding-inline : 1px ;
}
mfrac > * {
math-depth : auto-add;
math-style : compact;
}
mfrac > :nth-child (2 ) {
math-shift : compact;
}
<mfrac> 要素の フロー内 子が2つでない場合、そのレイアウトは
mrow フロー内 子を
分子 、
2番目は
分母
とし、下記のレイアウトアルゴリズムとなる。
根号要素 は、内容の上に線を持つ根号記号√を使った式を構成する。
msqrt 要素は
平方根に用いられ、mroot 要素は
たとえば立方根のように添字付きの根号に使われる。
<msqrt> および <mroot>
要素は
2.1.3 グローバル属性
次の例は
msqrt mroot msqrt mroot mroot
<math >
<mroot >
<msqrt >
<mfrac >
<mn > 1</mn >
<mn > 2</mn >
</mfrac >
<mo > +</mo >
<mn > 4</mn >
</msqrt >
<mn > 3</mn >
</mroot >
<mo > +</mo >
<mn > 0</mn >
</math >
<msqrt> および <mroot>
要素は math-shift を
compact に設定する。
<mroot> 要素は全ての子のうち最初の子以外に
scriptleveldisplaystyleユーザーエージェントスタイルシート
にはその挙動を実現するため次のルールが必須:
mroot > :not (:first-child ) {
math-depth : add (2 );
math-style : compact;
}
mroot, msqrt {
math-shift : compact;
}
<msqrt> や <mroot>
要素の計算された
display block math
または inline math でない場合、対応するCSS仕様に従ってレイアウトされる。
それ以外は以下レイアウトとなる。
<mroot> の フロー内 子が2つでない場合は
mrow フロー内 子を
mroot の基底
、2番目を
mroot の指数
と呼び、そのレイアウトアルゴリズムは下記。
<msqrt> 要素は
匿名 <mrow> ボックス
(msqrt
の基底 )を生成する。
歴史的に、
mstyle
要素は、その内容のレンダリングに影響するスタイル変更を行うために導入された。
<mstyle> 要素は
2.1.3 グローバル属性mrow
注
<mstyle> はフルMathMLとの互換性のために実装されている。MathML
Coreのみをターゲットとする場合は、スタイリングにCSSの利用が推奨される。
次の例では、
mstyle scriptlevel
およびdisplaystyle
の設定を行う。
これによって、それぞれ子孫のフォントサイズおよび添字の配置に影響が出ることがわかる。
MathML Core では
mrow
<math >
<munder >
<mo movablelimits ="true" > *</mo >
<mi > A</mi >
</munder >
<mstyle scriptlevel ="1" >
<mstyle displaystyle ="true" >
<munder >
<mo movablelimits ="true" > *</mo >
<mi > B</mi >
</munder >
<munder >
<mo movablelimits ="true" > *</mo >
<mi > C</mi >
</munder >
</mstyle >
<munder >
<mo movablelimits ="true" > *</mo >
<mi > D</mi >
</munder >
</mstyle >
</math >
merror
要素は内容を「エラーメッセージ」として表示する。この要素の意図は、他の入力からMathMLを生成するプログラムが入力の構文エラーを通知するための標準的な方法を提供することである。
次の例では
merror
<math >
<mfrac >
<merror >
<mtext > Syntax error: \frac{1}</mtext >
</merror >
<mn > 3</mn >
</mfrac >
</math >
<merror> 要素は
2.1.3 グローバル属性mrow ユーザーエージェントスタイルシート
にはエラーメッセージを視覚的に強調するため次のルールが必須:
merror {
border : 1px solid red;
background-color : lightYellow;
}
mpadded
要素は フロー内 子の内容と同じように描画されるが、
<mpadded> の属性に従い、その内容のサイズおよび相対位置の基準点が変更される。
<mpadded> 要素は
2.1.3 グローバル属性
width 、
height 、
depth 、
lspace
および
voffset
が存在する場合、その値は有効な <length-percentage>
でなければならない。
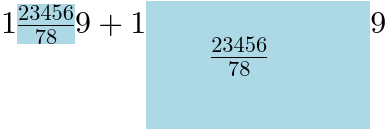
次の例では
mpadded mrow
<math >
<mrow >
<mn > 1</mn >
<mpadded style ="background: lightblue;" >
<mfrac >
<mn > 23456</mn >
<mn > 78</mn >
</mfrac >
</mpadded >
<mn > 9</mn >
</mrow >
<mo > +</mo >
<mrow >
<mn > 1</mn >
<mpadded lspace ="2em" voffset ="-1em" height ="1em" depth ="3em" width ="7em"
style ="background: lightblue;" >
<mfrac >
<mn > 23456</mn >
<mn > 78</mn >
</mfrac >
</mpadded >
<mn > 9</mn >
</mrow >
</math >
mpadded 匿名 <mrow> ボックス (
mpadded
内部ボックス )を生成し、
inner inline size・inner line-ascent ・inner line-descent というパラメータを持つ。
指定パラメータの決定方法:
指定幅は width プロパティの解決値。
width 属性が存在し有効かつパーセントでなければ、
その値で表示ヒント として
要素の width プロパティに設定。
height 属性が存在せず無効またはパーセントなら指定高さは
inner line-ascent 。
そうでなければheight属性の解決値(負値は0に丸める)。
depth 属性が存在せず無効またはパーセントなら指定depthは
inner line-ascent 。
そうでなければdepth属性の解決値(負値は0に丸める)。
lspace 属性が存在せず無効またはパーセントなら指定lspaceは0。そうでなければ解決値(負値は0に丸める)。
voffset 属性が存在せず無効またはパーセントなら指定voffsetは0。そうでなければ解決値。
注
voffset の負値は 0 に丸められない。
歴史的には、
mphantom
要素は、その内容を不可視状態で描画するが、内容を通常通りレンダリングした場合と同じ計量サイズや他の寸法(アルファベットベースライン の位置等を含む)を保持するために導入された。
次の例では
mphantom
<math >
<mfrac >
<mrow >
<mi > x</mi >
<mo > +</mo >
<mi > y</mi >
<mo > +</mo >
<mi > z</mi >
</mrow >
<mrow >
<mi > x</mi >
<mphantom >
<mo form ="infix" > +</mo >
<mi > y</mi >
</mphantom >
<mo > +</mo >
<mi > z</mi >
</mrow >
</mfrac >
</math >
<mphantom> 要素は
2.1.3
グローバル属性mrow ユーザーエージェントスタイルシート
では内容を不可視化するために、次のルールが必須である:
mphantom {
visibility : hidden;
}
注
<mphantom> はフルMathMLとの互換性のために実装されている。MathML
Coreのみをターゲットとする場合は、スタイリングにはCSS利用が推奨される。
このセクションで説明する要素は、基底の周囲に一つまたは複数のスクリプト(添え書き)を配置する。記号にさまざまな種類の添字や装飾を付けることは数学では非常に一般的な記法装置である。純粋な視覚的レイアウトだけなら、与えられた基底の周囲すべての伝統的なスクリプト位置にスクリプト・装飾を配置できる汎用要素ひとつで十分であろう。しかし一般的な記法の抽象構造をより明確に表現するため、MathMLではより専門化された複数のスクリプティング要素を提供している。
下付き・上付き要素に加えて、MathML には基底の上下にスクリプトを配置する overscript/underscript
要素がある。これらは大型演算子へのリミット設置や、基底の上・下へのアクセントやラインの配置に使うことができる。
msub ,
msup および
msubsup 要素は、
MathML式に添字(下付きや上付き)を付加するために使う。
これらは
2.1.3
グローバル属性
次の例は下付き添字と上付き添字の基本的な利用例。スクリプト内部では自動的にフォントサイズが縮小される。
<math >
<msub >
<mn > 1</mn >
<mn > 2</mn >
</msub >
<mo > +</mo >
<msup >
<mn > 3</mn >
<mn > 4</mn >
</msup >
<mo > +</mo >
<msubsup >
<mn > 5</mn >
<mn > 6</mn >
<mn > 7</mn >
</msubsup >
</math >
<msub>,
<msup> または
<msubsup> 要素の計算された
display block math
または inline math でない場合は、対応するCSS仕様に従ってレイアウトされる。
それ以外は以下のレイアウトとなる。
<msub> 要素の フロー内 子が2つでない場合、
mrow フロー内 子が
msub の基底 、
2番目が
msub
下付き と呼び、
レイアウトアルゴリズムは
3.4.1.2 下付き付き基底
<msup> 要素の フロー内 子が2つでない場合、
mrow フロー内 子が
msup の基底 、
2番目が
msup
上付き と呼び、
レイアウトアルゴリズムは
3.4.1.3 上付き付き基底
<msubsup> 要素の フロー内 子が3つでない場合、
mrow フロー内 子が
msubsup
の基底 、
2番目が msubsup 下付き 、
3番目が msubsup 上付き と呼び、
レイアウトアルゴリズムは
3.4.1.4
下付き・上付き付き基底
The munder ,
mover and
munderover elements are used to
attach
accents or limits placed under or over a MathML expression.
<munderover> 要素は
2.1.3
グローバル属性
同様に、<mover> 要素(それぞれ <munder> 要素)は
2.1.3
グローバル属性accent accentunder
accent ,
accentunder
属性は、存在する場合、その値が ブール値 でなければならない。
これらの属性が存在しないか無効な場合は false と見なされる。
ユーザーエージェントはこれらを
3.4.4
Displaystyle, scriptlevel and math-shift in scripts
The following example shows basic use of under- and overscripts.
The font-size is automatically scaled down within the scripts,
unless they are meant to be accents.
<math >
<munder >
<mn > 1</mn >
<mn > 2</mn >
</munder >
<mo > +</mo >
<mover >
<mn > 3</mn >
<mn > 4</mn >
</mover >
<mo > +</mo >
<munderover >
<mn > 5</mn >
<mn > 6</mn >
<mn > 7</mn >
</munderover >
<mo > +</mo >
<munderover accent ="true" >
<mn > 8</mn >
<mn > 9</mn >
<mn > 10</mn >
</munderover >
<mo > +</mo >
<munderover accentunder ="true" >
<mn > 11</mn >
<mn > 12</mn >
<mn > 13</mn >
</munderover >
</math >
If the
<munder>,
<mover> or
<munderover> elements do not have their
computed
display block math
or inline math
then they are laid out according to the CSS specification where
the corresponding value is described.
Otherwise, the layout below is performed.
すべての スクリプト要素 について、基本ルールは
1番目以外のすべての子要素に
displaystylefalse に設定し、
scriptlevelmover munderover accent ASCII 大文字・小文字問わず
true に一致する場合は
2番目(または3番目)の子内部で scriptlevel をインクリメントしない。さらに
mover munderover accentunder ASCII 大文字・小文字問わず
true に一致する場合も
2番目の子内部で scriptlevel をインクリメントしない。
<mmultiscripts> は
math-shiftcompact に、mprescripts の前なら偶数番目の子に、mprescripts 後なら奇数番目の子に適用。
<msub> および <msubsup>
は2番目の子に
math-shiftcompact に設定。
mover munderover accent ASCII 大文字・小文字問わず true の場合
1番目の子に math-shiftcompact を設定。
A. ユーザーエージェント
スタイルシート
msub > :not (:first-child ),
msup > :not (:first-child ),
msubsup > :not (:first-child ),
mmultiscripts > :not (:first-child ),
munder > :not (:first-child ),
mover > :not (:first-child ),
munderover > :not (:first-child ) {
math-depth : add (1 );
math-style : compact;
}
munder[accentunder="true" i] > :nth-child (2 ),
mover[accent="true" i] > :nth-child (2 ),
munderover[accentunder="true" i] > :nth-child (2 ),
munderover[accent="true" i] > :nth-child (3 ) {
font-size : inherit;
}
msub > :nth-child (2 ),
msubsup > :nth-child (2 ),
mmultiscripts > :nth-child (even),
mmultiscripts > mprescripts ~ :nth-child (odd),
mover[accent="true" i] > :first-child ,
munderover[accent="true" i] > :first-child {
math-shift : compact;
}
mmultiscripts > mprescripts ~ :nth-child (even) {
math-shift : inherit;
}
行列・配列その他表状の数式記法は
mtable mtr mtd table tr td HTML
以下の例は、表形式レイアウトにより行列を書けることを示す。分数の横棒や等号の中央と垂直に揃えられていることにも注目。
<math >
<mfrac >
<mi > A</mi >
<mn > 2</mn >
</mfrac >
<mo > =</mo >
<mrow >
<mo > (</mo >
<mtable >
<mtr >
<mtd > <mn > 1</mn > </mtd >
<mtd > <mn > 2</mn > </mtd >
<mtd > <mn > 3</mn > </mtd >
</mtr >
<mtr >
<mtd > <mn > 4</mn > </mtd >
<mtd > <mn > 5</mn > </mtd >
<mtd > <mn > 6</mn > </mtd >
</mtr >
<mtr >
<mtd > <mn > 7</mn > </mtd >
<mtd > <mn > 8</mn > </mtd >
<mtd > <mn > 9</mn > </mtd >
</mtr >
</mtable >
<mo > )</mo >
</mrow >
</math >
mtd は内容を中央揃えと既定のパディングにした
table-cell としてレイアウトされる。
ユーザーエージェントスタイルシート には
次のルールが必須:
mtd {
display : table-cell;
text-align : center;
padding : 0.5ex 0.4em ;
}
<mtd> は
2.1.3
グローバル属性
columnspanrowspancolspan rowspanHTML <td> 属性を踏襲。
特にパース方法は
行処理アルゴリズム に従い、
常に "colspan" を
"columnspan" と読替える。
注
[
MathML3 ]
以前ではこのカラム結合属性名は
columnspan であり、後方互換性保持のため残っている。
<mtd> 要素は
匿名 <mrow> ボックス を生成する。
歴史的に
maction
要素は、式にアクションをバインドする仕組みを提供する。
<maction> 要素は
2.1.3
グローバル属性
本仕様では、actiontype および selection
属性に特有の可観測な挙動を定義しない。
以下の例は [MathML3
<math >
<maction actiontype ="toggle" selection ="2" >
<mfrac >
<mn > 1</mn >
<mn > 2</mn >
</mfrac >
<mfrac >
<mn > 1</mn >
<mn > 3</mn >
</mfrac >
<mfrac >
<mn > 1</mn >
<mn > 4</mn >
</mfrac >
</maction >
</math >
<maction> のレイアウトアルゴリズムは <mrow> と同じである。
ユーザーエージェントスタイルシート
には、デフォルト動作(すなわち最初の子以外を隠す)を実装するため次のルールが必須:
maction > :not (:first-child ) {
display : none;
}
注
<maction> はフルMathMLとの互換性のために実装されている。MathML Core のみを対象とする著者は
独自アクション実装には他のHTML, CSS, JavaScript手法を推奨。
必要があれば [
MathML3 ]
で定義された maction 属性にも依拠できる。
semantics
要素は、MathML式に注釈を結びつけるためのコンテナ要素である。通常、
<semantics> 要素の最初の子は注釈対象となるMathML式であり、それ以降の子要素は
annotation
要素内のテキスト注釈、または
annotation-xml 要素内のより複雑なマークアップ注釈となる。
以下の例では分数「1/2」に一つはテキスト注釈(LaTeX)、もう一つはXML注釈(Content MathML)、さらにSVGやHTML注釈が加えられている。
これらはユーザーエージェントによる描画対象ではない。対応するSVGやHTMLマークアップも注釈として加えられている。
<math >
<semantics >
<mfrac >
<mn > 1</mn >
<mn > 2</mn >
</mfrac >
<annotation encoding ="application/x-tex" > \frac{1}{2}</annotation >
<annotation-xml encoding ="application/mathml-content+xml" >
<apply >
<divide />
<cn > 1</cn >
<cn > 2</cn >
</apply >
</annotation-xml >
<annotation-xml >
<svg width ="25" height ="75" xmlns ="http://www.w3.org/2000/svg" >
<path stroke-width ="5.8743"
d ="m5.9157 27.415h6.601v-22.783l-7.1813 1.4402v-3.6805l7.1408
-1.4402h4.0406v26.464h6.601v3.4005h-17.203z" />
<path stroke ="#000000" stroke-width ="2.3409"
d ="m0.83496 39.228h23.327" />
<path stroke-width ="5.8743"
d ="m8.696 70.638h14.102v3.4005h-18.963v-3.4005q2.3004-2.3804
6.2608-6.3813 3.9806-4.0206 5.0007-5.1808 1.9403-2.1803
2.7004-3.6805 0.78011-1.5202 0.78011-2.9804 0-2.3804
-1.6802-3.8806-1.6603-1.5002-4.3406-1.5002-1.9003 0-4.0206
0.6601-2.1003 0.6601-4.5007 2.0003v-4.0806q2.4404-0.98013
4.5607-1.4802 2.1203-0.50007 3.8806-0.50007 4.6407 0 7.401
2.3203 2.7604 2.3203 2.7604 6.2009 0 1.8403-0.7001 3.5006
-0.68013 1.6402-2.5004 3.8806-0.50007 0.58009-3.1805 3.3605
-2.6804 2.7604-7.5614 7.7412z" />
</svg >
</annotation-xml >
<annotation-xml encoding ="application/xhtml+xml" >
<div style ="display: inline-flex;
flex-direction: column; align-items: center;" >
<div > 1</div >
<div > ―</div >
<div > 2</div >
</div >
</annotation-xml >
</semantics >
</math >
<semantics> 要素は
2.1.3 グローバル属性mrow ユーザーエージェントスタイルシート
には、注釈付きのMathML式(最初の子)のみ描画対象とするため次のルールが必須:
semantics > :not (:first-child ) {
display : none;
}
<annotation-xml> および
<annotation> 要素は
2.1.3 グローバル属性
本仕様では encoding
属性に特有の可観測な挙動を定義しない。
<annotation-xml> および <annotation> の
レイアウトアルゴリズムは
mtext
注
著者は
encoding
属性を使い、HTMLインテグレーションポイントやクリップボードコピー、代替レンダリングなど用途で注釈を区別できる。
特にCSSで代替注釈を描画可能。例:
semantics > :first-child { display : none; }
semantics > annotation { display : inline; }
semantics > annotation-xml[encoding="text/html" i] ,
semantics > annotation-xml[encoding="application/xhtml+xml" i] {
display : inline-block;
}
display プロパティ
CSS Display Module Level 3
MathML要素 でない要素の場合、
指定値が display: block math や
display: inline math なら、計算値は
block flow、inline flow となる。
mtable block table、
inline table。
mtr table-row。
mtd table-cell。
計算済 display 値が
block math や inline math の
MathML要素 は、
タグ名等に応じたボックス生成・レイアウトを行う。
未知のMathML要素
は
mrow
注
display: block math と
display: inline math はMathML要素のデフォルトレイアウトを提供する一方、
ネイティブdisplay値や
カスタム値
でこれを上書き可能。
これにより記法拡張やPolyfill等のカスタム表記も実現できる。
以下の例は、MathML
mrow
<math >
<msup >
<mrow >
<mo symmetric ="false" > [</mo >
<mrow style ="display: block; width: 4.5em;" >
<mrow style ="display: grid;
grid-template-columns: 1.5em 1.5em 1.5em;
grid-template-rows: 1.5em 1.5em;
justify-items: center;
align-items: center;" >
<mn > 12</mn >
<mn > 34</mn >
<mn > 56</mn >
<mn > 7</mn >
<mn > 8</mn >
<mn > 9</mn >
</mrow >
</mrow >
<mo symmetric ="false" > ]</mo >
</mrow >
<mi > α</mi >
</msup >
</math >
math-style が compact の場合、子孫の数式レイアウトは
logical height の最小化を目指し、以下を適用する:
次の例は
math math-style: compact(左)と
math-style: normal(右)を設定した数式レンダ例。
前者では分数内フォント縮小とΣの制限が下付き・上付きとして描画され、後者ではΣが大型化、分数内空きも増加した。
2つの math-style 値は、典型的にインライン(compact)/ディスプレイ(normal)モード式に対応
[TeXBook math-style プロパティでユーザエージェントスタイルシートや
displaystyle 属性から
簡単にこの挙動を制御・Polyfill等で拡張できる。
数式各要素についてトップレベルからの「深さ」を記述する
math-depth プロパティが導入される。これは
font-size 指定値が math の場合の
計算値決定等に使われる。
math-depth の計算値判定手順:
指定値が auto-add かつ
継承 math-style
が compact なら、計算値は継承値+1
指定値が add(<integer>) なら、計算値は継承値+指定整数
指定値が整数なら、計算値はその整数
その他は継承値
font-size 指定値が math の場合、
計算値は継承 font-size × 下記手順のスケールファクタとなる:
A=継承 math-depth 、
B=計算 math-depth 、
C=0.71、S=1.0とする
A=BならSを返す
B < A ならA,BをswapしInvertScaleFactor=true
それ以外はB>AでInvertScaleFactor=false
E=B-A > 0
継承フォントにOpenType MATHテーブルがあれば:
S×CE
InvertScaleFactor=falseならS、trueなら1/Sを返す
下例は
通常 math-style
の数式がLatin Modern Mathフォントで表示される例。
スクリプトや分数などの部分式でフォントサイズが自動縮小されていく。
上付きでは縮小、ルート内部(prescript)ではさらに急速に縮小、分数も内側は縮小だが外側は
math-style 自動切替のため縮小しない等がわかる。
[TeXBook math-depth
機構で実装可能なことは重要。
MathMLなら ユーザーエージェントスタイルシート でも適用できる。
Polyfill等の調整にも有用。 MathMLの scriptlevel 属性
で math-depth 変更も可能。
本章ではOpenTypeフォントの MATH テーブル
[OPEN-FONT-FORMAT Table.Subtable1[index].Subtable2.Parameter
を用いてOpenTypeパラメータを指す。
こうしたパラメータは(サブテーブルが無い・オフセット不正など)利用できない場合もあるため、フォールバック手段が準備されている。
注
MathMLは適切なOpenType機能を持つ数学フォントで描画することが強く推奨される。ここで用意されるフォールバックでは十分良い描画が保証されない場合がある。
OpenType値(間接的にMathValueRecord経由も含む)がデザイン単位で与えられる場合、レイアウト用途で
head.unitsPerEm、CSS
font-size
またはズーム値を加味して適切な値にスケーリングされる。
以下は
最初に利用可能なフォント に対する全体のレイアウト定数である。
デフォルト・フォールバック定数 0
デフォルト罫線太さ
post.underlineThickness もしくは
デフォルト・フォールバック定数 (定数未定義時)。
scriptPercentScaleDown
MATH.MathConstants.scriptPercentScaleDown / 100 もしくは
MATH.MathConstants.scriptPercentScaleDown が null/無い場合は0.71
scriptScriptPercentScaleDown
MATH.MathConstants.scriptScriptPercentScaleDown / 100 または
null/値なしの時は0.5041
displayOperatorMinHeight MATH.MathConstants.displayOperatorMinHeight もしくは
定数未定義時はデフォルト・フォールバック定数
axisHeight
MATH.MathConstants.axisHeight または 定数未定義時 OS/2.sxHeight の半分accentBaseHeight MATH.MathConstants.accentBaseHeight または無い場合 OS/2.sxHeightsubscriptShiftDown MATH.MathConstants.subscriptShiftDown または無い場合 OS/2.ySubscriptYOffsetsubscriptTopMax MATH.MathConstants.subscriptTopMax または 無い場合 ⅘ × OS/2.sxHeightsubscriptBaselineDropMin
MATH.MathConstants.subscriptBaselineDropMin またはデフォルト・フォールバック定数
superscriptShiftUp MATH.MathConstants.superscriptShiftUp または OS/2.ySuperscriptYOffset(無い時)
superscriptShiftUpCramped
MATH.MathConstants.superscriptShiftUpCramped またはデフォルト・フォールバック定数
superscriptBottomMin MATH.MathConstants.superscriptBottomMin または無い時 ¼ × OS/2.sxHeightsuperscriptBaselineDropMax MATH.MathConstants.superscriptBaselineDropMax またはデフォルト・フォールバック定数
subSuperscriptGapMin
MATH.MathConstants.subSuperscriptGapMin または未定義時は4 × デフォルト罫線太さ
superscriptBottomMaxWithSubscript MATH.MathConstants.superscriptBottomMaxWithSubscript または未定義時 ⅘ ×
OS/2.sxHeight
spaceAfterScript MATH.MathConstants.spaceAfterScript または未定義時 1/24emupperLimitGapMin MATH.MathConstants.upperLimitGapMin または未定義時デフォルト・フォールバック定数
upperLimitBaselineRiseMin MATH.MathConstants.upperLimitBaselineRiseMin または未定義時デフォルト・フォールバック定数 lowerLimitGapMin MATH.MathConstants.lowerLimitGapMin または未定義時デフォルト・フォールバック定数
lowerLimitBaselineDropMin MATH.MathConstants.lowerLimitBaselineDropMin または未定義時デフォルト・フォールバック定数 stackTopShiftUp MATH.MathConstants.stackTopShiftUp または未定義時デフォルト・フォールバック定数 stackTopDisplayStyleShiftUp MATH.MathConstants.stackTopDisplayStyleShiftUp またはデフォルト・フォールバック定数 stackBottomShiftDown MATH.MathConstants.stackBottomShiftDown またはデフォルト・フォールバック定数 stackBottomDisplayStyleShiftDown MATH.MathConstants.stackBottomDisplayStyleShiftDown またはデフォルト・フォールバック定数 stackGapMin
MATH.MathConstants.stackGapMin または未定義時 3 × デフォルト罫線太さ
stackDisplayStyleGapMin MATH.MathConstants.stackDisplayStyleGapMin または未定義時 7 × デフォルト罫線太さ stretchStackTopShiftUp MATH.MathConstants.stretchStackTopShiftUp またはデフォルト・フォールバック定数 stretchStackBottomShiftDown MATH.MathConstants.stretchStackBottomShiftDown またはデフォルト・フォールバック定数 stretchStackGapAboveMin MATH.MathConstants.stretchStackGapAboveMin またはデフォルト・フォールバック定数 stretchStackGapBelowMin MATH.MathConstants.stretchStackGapBelowMin またはデフォルト・フォールバック定数 fractionNumeratorShiftUp MATH.MathConstants.fractionNumeratorShiftUp またはデフォルト・フォールバック定数 (未定義時)fractionNumeratorDisplayStyleShiftUp MATH.MathConstants.fractionNumeratorDisplayStyleShiftUp またはデフォルト・フォールバック定数 fractionDenominatorShiftDown MATH.MathConstants.fractionDenominatorShiftDown またはデフォルト・フォールバック定数 fractionDenominatorDisplayStyleShiftDown MATH.MathConstants.fractionDenominatorDisplayStyleShiftDown またはデフォルト・フォールバック定数 fractionNumeratorGapMin MATH.MathConstants.fractionNumeratorGapMin またはデフォルト罫線太さ
fractionNumDisplayStyleGapMin MATH.MathConstants.fractionNumDisplayStyleGapMin または未定義時 3 × デフォルト罫線太さ fractionRuleThickness MATH.MathConstants.fractionRuleThickness またはデフォルト罫線太さ
fractionDenominatorGapMin MATH.MathConstants.fractionDenominatorGapMin またはデフォルト罫線太さ
fractionDenomDisplayStyleGapMin MATH.MathConstants.fractionDenomDisplayStyleGapMin または未定義時 3 × デフォルト罫線太さ overbarVerticalGap MATH.MathConstants.overbarVerticalGap または未定義時 3 × デフォルト罫線太さ
MATH.MathConstants.overbarExtraAscender またはデフォルト罫線太さ underbarVerticalGap MATH.MathConstants.underbarVerticalGap または未定義時 3 × デフォルト罫線太さ MATH.MathConstants.underbarExtraDescender またはデフォルト罫線太さ radicalVerticalGap MATH.MathConstants.radicalVerticalGap または未定義時 1¼ × デフォルト罫線太さ radicalDisplayStyleVerticalGap MATH.MathConstants.radicalDisplayStyleVerticalGap またはデフォルト罫線太さ + ¼
OS/2.sxHeight(未定義時)
radicalRuleThickness MATH.MathConstants.radicalRuleThickness またはデフォルト罫線太さ MATH.MathConstants.radicalExtraAscender またはデフォルト罫線太さ radicalKernBeforeDegree MATH.MathConstants.radicalKernBeforeDegree または未定義時 5/18emradicalKernAfterDegree MATH.MathConstants.radicalKernAfterDegree または未定義時 −10/18emradicalDegreeBottomRaisePercent MATH.MathConstants.radicalDegreeBottomRaisePercent / 100.0 または未定義時 0.6
このセクションでは MATH.MathVariants テーブルを用いた任意サイズのストレッチグリフ処理について説明する。
本節は [OPEN-TYPE-MATH-IN-HARFBUZZ
omin
=
MATH.MathVariant.minConnectorOverlap
GlyphPartRecord が fExtender フラグ有なら extender である。
MathVariant.horizGlyphConstructionOffsets より得たら横組 、それ以外は縦組
与えられた GlyphAssembly について、
NExt
(および
NNonExt )は
extender(およびextenderでない)数
同じく
SExt
(SNonExt )は
extender(非extender)のfullAdvance和
SExt,NonOverlapping = SExt − omin NExt
以下成立しない場合、user agentはGlyphAssemblyを無効とみなす:
本仕様では各extenderをr回繰り返し、各グリフ間overlapをoとして組み立てる。
glyph数は
AssemblyGlyphCount (r) = NNonExt + r NExt
伸長サイズは
AssembySize (o, r) =
SNonExt + r SExt
− o(AssemblyGlyphCount (r) − 1)
rmin は
要求サイズ T に到達するためのrepetition数の最小値:
AssembySize (omin , r) ≥ T
となる最小r。max(0, ceil((T − SNonExt + omin (NNonExt −1))/SExt,NonOverlapping )
omax,theorical = (AssembySize (0, rmin ) − T)/(AssemblyGlyphCount (rmin ) − 1)
omax
は
extenderをrmin 回繰返すことで
T以上のサイズを作る最大overlap値:
AssemblyGlyphCount (rmin ) ≤ 1 なら
overlap値は何でも良い。それ以外は以下最小:
omax,theorical
GlyphPartRecord.startConnectorLength 各値(最後の非extenderを除く)
GlyphPartRecord.endConnectorLength 各値(最初の非extenderを除く)
指定サイズ Tに対する glyph assembly stretch size
は
AssembySize (omax , rmin )
glyph
assembly width 、
glyph
assembly ascent
glyph
assembly descent
は以下の通り:
縦組みの場合
幅=partRecords中すべての
GlyphPartRecord.glyphID の進行幅最大値
ascent=stretch size
descent=0
横組みの場合
幅=stretch size
ascent/descent=partRecords内各グリフIDのascent/descent最大値
glyph
assembly height =
glyph assembly ascent +
glyph assembly descent
注
縦組み(または横組み) glyph assembly の横(縦)メトリックはTに依存しない。
glyph assembly の shaping
アルゴリズムは以下:
rmin と
omax 決定
(x, y)=(0, 0)、RepetitionCounter=0、PartIndex=-1に
以下繰り返す:
RepetitionCounter==0なら
PartIndex++PartIndex==partCountなら 終了
それ以外はPart=partRecords[PartIndex]、extenderならRepetitionCounter=rmin、非なら1
横組なら glyph(Part.glyphID)を(x,y)左・ベースライン位置に描画
x=x+fullAdvance−omax
縦組なら glyph(Part.glyphID)を(x, y)左・下端に描画
y=y−fullAdvance+omax
RepetitionCounter--
block軸伸長グリフの望ましいインラインサイズ
はこのアルゴリズムで決定:
S=グリフの進行幅
MathGlyphConstructionテーブルが MathVariants.vertGlyphConstructionOffsets
にあれば
各MathGlyphVariantRecordについて、SをvariantGlyphの進行幅最大値に
有効なGlyphAssemblyがあれば
Sを assembly width 以上に
Sを返す
注
block軸伸長グリフの望ましいインラインサイズは、全ての縦伸長構成の最大幅を返す。
実際、数学フォントは縦組構成がほぼ一定幅なので過大評価は小さい。
グリフをインライン/ブロック方向Tにストレッチ成形 するアルゴリズムは以下:
MathGlyphConstructionテーブルが無い場合は失敗で終了
グリフ進行幅(または高さ)がT以上なら通常成形でそのグリフ・MathItalicsCorrectionInfo・バウンディングボックスで成功
MathGlyphVariantRecordにadvanceMeasurementがT以上のものがあれば
そのvariantGlyph・MathItalicsCorrectionInfo・通常成形で成功
有効なGlyphAssemblyがあれば、指定b.box・GlyphAssembly.italicsCorrectionで shaping を行い成功
Stretch方でTに届かなければ直前の結果で成功
@namespace url(http ://www.w3.org/1998 /Math/MathML);
* {
font-size : math;
display : block math;
writing-mode : horizontal-tb !important ;
}
math {
direction : ltr;
text-indent : 0 ;
letter-spacing : normal;
line-height : normal;
word-spacing : normal;
font-family : math;
font-size : inherit;
font-style : normal;
font-weight : normal;
display : inline math;
math-shift : normal;
math-style : compact;
math-depth : 0 ;
}
math[display="block" i] {
display : block math;
math-style : normal;
}
math[display="inline" i] {
display : inline math;
math-style : compact;
}
semantics > :not (:first-child ) {
display : none;
}
maction > :not (:first-child ) {
display : none;
}
merror {
border : 1px solid red;
background-color : lightYellow;
}
mphantom {
visibility : hidden;
}
mi {
text-transform : math-auto;
}
mtable {
display : inline-table;
math-style : compact;
}
mtr {
display : table-row;
}
mtd {
display : table-cell;
text-align : center;
padding : 0.5ex 0.4em ;
}
mfrac {
padding-inline : 1px ;
}
mfrac > * {
math-depth : auto-add;
math-style : compact;
}
mfrac > :nth-child (2 ) {
math-shift : compact;
}
mroot > :not (:first-child ) {
math-depth : add (2 );
math-style : compact;
}
mroot, msqrt {
math-shift : compact;
}
msub > :not (:first-child ),
msup > :not (:first-child ),
msubsup > :not (:first-child ),
mmultiscripts > :not (:first-child ),
munder > :not (:first-child ),
mover > :not (:first-child ),
munderover > :not (:first-child ) {
math-depth : add (1 );
math-style : compact;
}
munder[accentunder="true" i] > :nth-child (2 ),
mover[accent="true" i] > :nth-child (2 ),
munderover[accentunder="true" i] > :nth-child (2 ),
munderover[accent="true" i] > :nth-child (3 ) {
font-size : inherit;
}
msub > :nth-child (2 ),
msubsup > :nth-child (2 ),
mmultiscripts > :nth-child (even),
mmultiscripts > mprescripts ~ :nth-child (odd),
mover[accent="true" i] > :first-child ,
munderover[accent="true" i] > :first-child {
math-shift : compact;
}
mmultiscripts > mprescripts ~ :nth-child (even) {
math-shift : inherit;
}
カテゴリから演算子のプロパティを設定するアルゴリズム は次の通り:
minsize を 100% に設定。maxsize を ∞ に設定。指定カテゴリに対応する行を図
26 で探す。
lspace および rspace を対応列で指定された値に設定。各プロパティ(stretchy、symmetric、largeop、movablelimits)について、最後の列に列挙されていればtrue、なければfalseを設定。
演算子のカテゴリ決定アルゴリズム
(Content, Form) は以下の通り:
Content(UTF-16文字列)の長さが1または2でなければ、カテゴリDefaultで打ち切り。
ContentがU+0320–U+03FFの範囲内1文字なら、カテゴリDefaultで打ち切り。2文字の場合は:
Contentが
U+1EEF0 ARABIC MATHEMATICAL OPERATOR MEEM WITH HAH WITH TATWEEL
または U+1EEF1 ARABIC MATHEMATICAL OPERATOR HAH WITH DAL のサロゲートペアで
且つ Form が postfix なら、カテゴリIで打ち切り。
2文字目が
U+0338 COMBINING LONG SOLIDUS OVERLAY または
U+20D2 COMBINING LONG VERTICAL LINE OVERLAY なら
Content を1文字目に置き換え、手順3へ。
それ以外で Content が
Operators_2_ascii_charsContentを
「U+0320 + インデックス」に置換え手順3へ。
他はカテゴリDefaultで打ち切り。
Formがinfixで ContentがU+007C またはU+223C ならカテゴリForceDefaultで打ち切り。
(Content, Form)のカテゴリが
図
25
でN/A符号化(カテゴリL/M)なら、そのカテゴリで打ち切り。
それ以外は:
U+0000–U+03FF内ならKey=Content、
U+2000–U+2BFF内ならKey=Content−0x1C00。
他はDefaultで打ち切り。
Formがinfix/prefix/postfixならそれぞれ0x0000/0x1000/0x2000をKeyに加算。アサート :
Keyは0x2FFF以下。
図
27 で
Entry%0x4000=KeyのEntryを探し、
見つかれば
図
26 でencodingからカテゴリ返し、なければDefault。
特殊表
エントリ数
Operators_2_ascii_chars18エントリ(2文字ASCII):'!!', '!=', '&&', '**', '*=', '++', '+=', '--', '-=', '->', '//', '/=', ':=', '<=', '<>', '==', '>=', '||',
Operators_fence61エントリ(16範囲):[U+0028–U+0029], {U+005B}, {U+005D}, [U+007B–U+007D], {U+0331}, {U+2016}, [U+2018–U+2019], [U+201C–U+201D], [U+2308–U+230B], [U+2329–U+232A], [U+2772–U+2773], [U+27E6–U+27EF], {U+2980}, [U+2983–U+2999], [U+29D8–U+29DB], [U+29FC–U+29FD},
Operators_separator3エントリ:U+002C, U+003B, U+2063,
図 24 演算子辞書の特殊テーブル。
(Content, Form)キー
カテゴリ
中置(infix )313件(35範囲):[U+2190–U+2195], [U+219A–U+21AE], [U+21B0–U+21B5], {U+21B9}, ...
A
中置108件(31範囲):{U+002B}, {U+002D}, ...
B
中置64件(33範囲):{U+0025}, {U+002A}, ...
C
前置(prefix )52件(22範囲):{U+0021}, ...
D
後置(postfix )40件(21範囲):[U+0021–U+0022], ...
E
前置30件:U+0028, U+005B, ...
F
後置30件:U+0029, U+005D, ...
G
前置27件(2範囲):[U+222B–U+2233], ...
H
後置22件(13範囲):[U+005E–U+005F], ...
I
前置22件(6範囲):[U+220F–U+2211], ...
J
中置8件(5範囲):{U+002F}, {U+005C}, ...
K
前置6件(3範囲):[U+2145–U+2146], ...
L
中置3件:U+002C, U+003A, U+003B,
M
図 25 演算子(Content, Form)からカテゴリへの対応表。
カテゴリ
形式
符号
lspace
rspace
プロパティ
Default
N/A
N/A
0.2777777777777778em0.2777777777777778emN/A
ForceDefault
N/A
N/A
0.2777777777777778em0.2777777777777778emN/A
A
中置
0x0
0.2777777777777778em0.2777777777777778emstretchy
B
中置
0x4
0.2222222222222222em0.2222222222222222emN/A
C
中置
0x8
0.16666666666666666em0.16666666666666666emN/A
D
前置
0x1
00N/A
E
後置
0x2
00N/A
F
前置
0x5
00stretchy symmetric
G
後置
0x6
00stretchy symmetric
H
前置
0x9
0.16666666666666666em0.16666666666666666emsymmetric largeop
I
後置
0xA
00stretchy
J
前置
0xD
0.16666666666666666em0.16666666666666666emsymmetric largeop movablelimits
K
中置
0xC
00N/A
L
前置
N/A
0.16666666666666666em0N/A
M
中置
N/A
00.16666666666666666emN/A
図 26 各カテゴリに対する演算子の値。
716件(236範囲, 範囲長最大16):
{0x8025}, {0x802A}, {0x402B}, ...
図 27 Key=Entry%0x4000,
category=Entry/0x1000。
注
図
25 および
図
27
は連続するUnicodeブロックにあわせて範囲化されている。
検索の際は範囲開始で二分探索+範囲長で追加判定を用いると速い
logは凹関数ゆえに
図
27
全体で一度二分探索する方が
図
25
の各大サブ表毎に探索するより効率的。
文字cの本来のストレッチ軸 は下記リストの文字ならインライン軸 。
それ以外はブロック軸 。
U+003D,
U+005E,
U+005F,
U+007E,
U+00AF,
U+02C6,
U+02C7,
U+02C9,
U+02CD,
U+02DC,
U+02F7,
U+0302,
U+0332,
U+203E,
U+20D0,
U+20D1,
U+20D6,
U+20D7,
U+20E1,
U+2190,
U+2192,
U+2194,
U+2198,
U+2199,
U+219A,
U+219B,
U+219C,
U+219D,
U+219E,
U+21A0,
U+21A2,
U+21A3,
U+21A4,
U+21A6,
U+21A9,
U+21AA,
U+21AB,
U+21AC,
U+21AD,
U+21AE,
U+21B4,
U+21B9,
U+21BC,
U+21BD,
U+21C0,
U+21C1,
U+21C4,
U+21C6,
U+21C7,
U+21C9,
U+21CB,
U+21CC,
U+21CD,
U+21CE,
U+21CF,
U+21D0,
U+21D2,
U+21D4,
U+21DA,
U+21DB,
U+21DC,
U+21DD,
U+21E0,
U+21E2,
U+21E4,
U+21E5,
U+21E6,
U+21E8,
U+21F0,
U+21F4,
U+21F6,
U+21F7,
U+21F8,
U+21F9,
U+21FA,
U+21FB,
U+21FC,
U+21FD,
U+21FE,
U+21FF,
U+2322,
U+2323,
U+23B4,
U+23B5,
U+23DC,
U+23DD,
U+23DE,
U+23DF,
U+23E0,
U+23E1,
U+2500,
U+2794,
U+2799,
U+279B,
U+279C,
U+279D,
U+279E,
U+279F,
U+27A0,
U+27A1,
U+27A5,
U+27A6,
U+27A8,
U+27A9,
U+27AA,
U+27AB,
U+27AC,
U+27AD,
U+27AE,
U+27AF,
U+27B1,
U+27B3,
U+27B5,
U+27B8,
U+27BA,
U+27BB,
U+27BC,
U+27BD,
U+27BE,
U+27F4,
U+27F5,
U+27F6,
U+27F7,
U+27F8,
U+27F9,
U+27FA,
U+27FB,
U+27FC,
U+27FD,
U+27FE,
U+27FF,
U+2900,
U+2901,
U+2902,
U+2903,
U+2904,
U+2905,
U+2906,
U+2907,
U+290C,
U+290D,
U+290E,
U+290F,
U+2910,
U+2911,
U+2914,
U+2915,
U+2916,
U+2917,
U+2918,
U+2919,
U+291A,
U+291B,
U+291C,
U+291D,
U+291E,
U+291F,
U+2920,
U+2942,
U+2943,
U+2944,
U+2945,
U+2946,
U+2947,
U+2948,
U+294A,
U+294B,
U+294E,
U+2950,
U+2952,
U+2953,
U+2956,
U+2957,
U+295A,
U+295B,
U+295E,
U+295F,
U+2962,
U+2964,
U+2966,
U+2967,
U+2968,
U+2969,
U+296A,
U+296B,
U+296C,
U+296D,
U+2970,
U+2971,
U+2972,
U+2973,
U+2974,
U+2975,
U+297C,
U+297D,
U+2B04,
U+2B05,
U+2B0C,
U+2B30,
U+2B31,
U+2B32,
U+2B33,
U+2B34,
U+2B35,
U+2B36,
U+2B37,
U+2B38,
U+2B39,
U+2B3A,
U+2B3B,
U+2B3C,
U+2B3D,
U+2B3E,
U+2B40,
U+2B41,
U+2B42,
U+2B43,
U+2B44,
U+2B45,
U+2B46,
U+2B47,
U+2B48,
U+2B49,
U+2B4A,
U+2B4B,
U+2B4C,
U+2B60,
U+2B62,
U+2B64,
U+2B6A,
U+2B6C,
U+2B70,
U+2B72,
U+2B7A,
U+2B7C,
U+2B80,
U+2B82,
U+2B84,
U+2B86,
U+2B95,
U+FE35,
U+FE36,
U+FE37,
U+FE38,
U+1EEF0,
U+1EEF1,
図 28
インラインストレッチ軸を持つ演算子コードポイント(昇順)
注
本来のストレッチ軸は、演算子辞書の真偽値プロパティとして持たせることも可能だが
形態に依存せず、ごく一部の演算子のみインライン軸ストレッチがあるため
独立の昇順配列で実装する方が良い。サロゲートペア(U+1EEF0, U+1EEF1)は個別判定推奨。
↑