以下の注意事項は、SVG言語の機能で要求されるフォーマットへのコンテンツ変換や、そこからの変換を行う際に、ソフトウェア開発者が利用できるアルゴリズムやその他の手法について説明します。
他のパスセグメント表記と一貫性を持たせるため、SVGパス内の弧は曲線上の開始点と終了点で定義されます。
この楕円弧のパラメータ化はエンドポイントパラメータ化と呼ばれます。エンドポイントパラメータ化の利点のひとつは、すべてのパスコマンドが新しい「現在の点」の座標で終わるという一貫したパス構文を可能にすることです。
しかし、これはソフトウェアや数学で弧の幾何を記述する唯一の方法ではありません。 この節では、もう一つの中心パラメータ化について説明し、SVGのエンドポイントパラメータ化との相互変換方法も示します。
SVGパスコマンドで表される楕円弧は、以下のパラメータで順番に記述されます:
(x1, y1)は、パス上の現在の点の絶対座標で、前のパスコマンドの最後の2つのパラメータから取得されます。
rx およびry は楕円の半径(主軸・副軸とも呼ばれます)です。
φは、現在の座標系のx軸から楕円のx軸への角度です。
fAは ラージアークフラグで、180度以下の弧を選択する場合は0、180度を超える弧を選択する場合は1です。
fSは スウィープフラグで、中心から弧への線が減少方向に角度を移動する場合は0、増加方向の場合は1です。
(x2, y2)は弧の終点の絶対座標です。
楕円弧上の任意の点(x, y)は、次の2次元行列式で表せます:
(eq. 3.1)
x = rx*cos(θ)*cos(φ) - ry*sin(θ)*sin(φ) + cx
y = rx*cos(θ)*sin(φ) + ry*sin(θ)*cos(φ) + cy
(cx, cy)は楕円の中心座標です。
rxおよびryは楕円の半径(主軸・副軸とも呼ばれます)です。
φは現在の座標系のx軸から楕円のx軸への角度です。
θは弧上の点(x, y)が位置する弧周上の角度で、次の範囲になります:
楕円を伸ばして回転させた円と考える場合、θ1、θ2、Δθはストレッチ・回転前の開始角・終了角・スウィープ角となります。 これはグラフィックスAPIで一般的な別のパラメータ化につながり、中心パラメータ化と呼ばれます。次節では中心パラメータ化とエンドポイントパラメータ化の相互変換式を示します。
次の変数が与えられます:
cx cy rx ry φ θ1 Δθ
求めるべきは以下です:
x1 y1 x2 y2 fA fS
これらは以下の式を使って求めることができます:
|
|
(式 4.1) |
|
|
(式 4.2) |
|
|
(式 4.3) |
|
|
(式 4.4) |
次の変数が与えられます:
x1 y1 x2 y2 fA fS rx ry φ
求めるべきは以下です:
cx cy θ1 Δθ
式は、(x1, y1)から(x2, y2)への線分の中点に原点を移動し、座標軸を楕円の軸に合わせて回転することで簡略化されます。 変換後の座標はプライム記号で表記され、中間値として求められます。この手順は以下のステップで構成されます:
ステップ1: 計算 (x1′, y1′)
|
|
(式 5.1) |
ステップ2: 計算 (cx′, cy′)
|
|
(式 5.2) |
ここで、+記号はfA ≠ fSの場合に選択し、−記号はfA = fSの場合に選択します。
ステップ3: 計算 (cx, cy) from (cx′, cy′)
|
|
(式 5.3) |
ステップ4: 計算 θ1 および Δθ
一般に、2つのベクトル(ux, uy)と(vx, vy)間の角度は次式で求められます:
|
|
(式 5.4) |
この±記号は、ux vy − uy vxの符号です。
この角度関数を用いて、θ1 および Δθ は以下で表されます:
|
|
(式 5.5) |
|
|
(式 5.6) |
ここでΔθは −360° < Δθ < 360°の範囲で次を満たします:
もしfS = 0ならΔθ < 0,
もしfS = 1ならΔθ > 0.
つまり、fS = 0で(式 5.6)の右辺が0より大きければ360°を減算し、fS = 1で右辺が0より小さければ360°を加算します。それ以外はそのままにします。
この節では、パス実装に関する注意で説明されている範囲外のrxおよび ryに対して必要な数学的調整について説明します。 アルゴリズムとしては、以下のステップで構成されます:
ステップ1: 半径がゼロでないことを確認する
もしrx = 0 または ry = 0 であれば、 (x1, y1)から(x2, y2)への直線として扱い、処理を終了します。そうでなければ、
ステップ2: 半径が正であることを確認する
rxとryの絶対値を取得します:
|
|
(式 6.1) |
ステップ3: 半径が十分大きいことを確認する
式(式 5.1)のプライム座標値を用いて、以下を計算します
|
|
(式 6.2) |
上記の式の結果が1以下であれば、rxおよびryはさらに変更する必要はありません。 上記の式の結果が1より大きい場合、以下のように置き換えます:
|
|
(式 6.3) |
ステップ4: 計算を続行する
残りの楕円弧計算(エンドポイントから中心へのパラメータ変換アルゴリズムなど)を続行します。 注意:この節の半径補正の結果、楕円の中心を求める式(式 5.2)は常に少なくとも1つの解を持ちます(根号内は絶対に負になりません)。もし式(式 6.3)で半径が拡大される場合、式(式 5.2)の根号内は0となり、楕円の中心の解はちょうど1つだけになります。
この節は参考情報です。
SVGの実数精度は単精度です。 技術データを扱う適合SVG生成器で、単精度を超える情報表現が必要な場合(地図や技術図面など)には、一貫した表示を適合SVGビューアで保証するため、この節で説明されている手順に従うことが推奨されます。
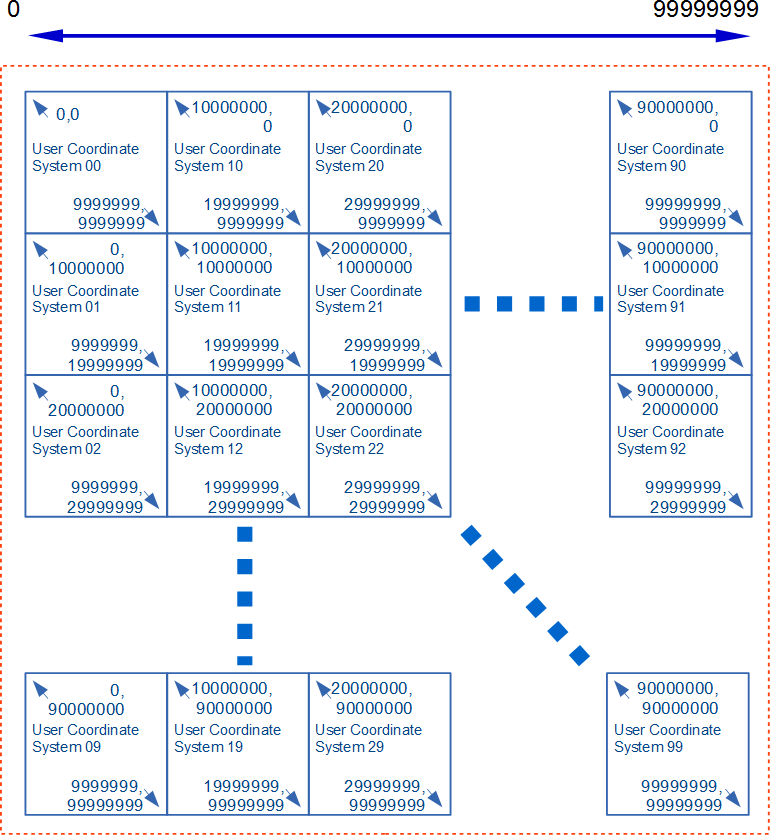
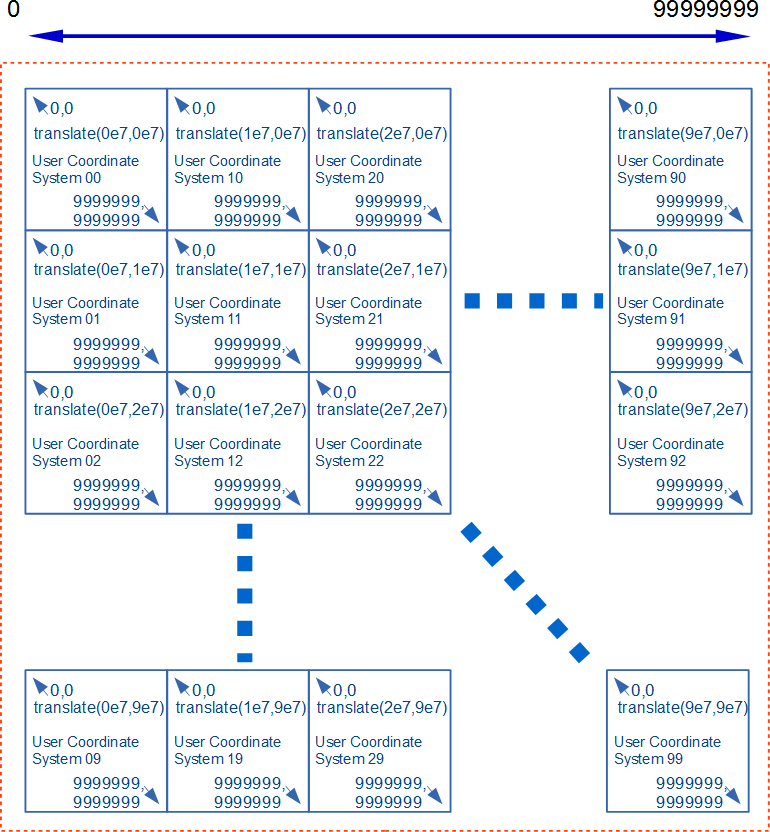
単精度よりも高い有効精度で表示したい場合は、CTM生成時に少なくとも倍精度浮動小数点が使用されることを利用することで可能となります(適合SVGビューア節のCTM生成処理参照)。 これを活用したコンテンツ生成手順は次の通りです:
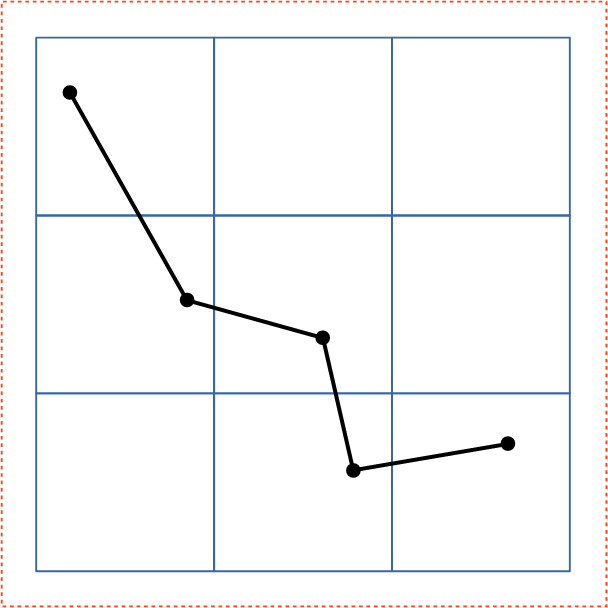
| 分割前 | 分割後 | |
|---|---|---|
 |
 |
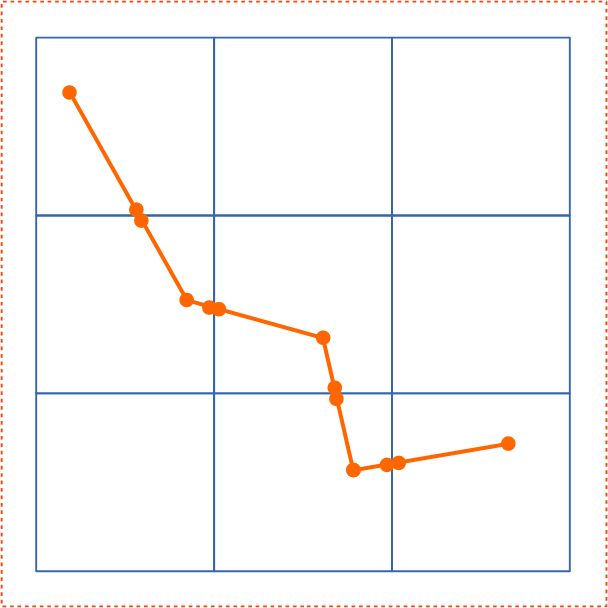
| ステップ1:分割 | ステップ5:有効桁数を小さくしつつ適切な配置 | |
|---|---|---|
 |
 |
|
| この例ではユーザー座標系が7桁のタイルを用いることで8桁の有効数字を提供しています。 | ||